
 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案 課時掌控隨堂練習系列答案
課時掌控隨堂練習系列答案 一課一練一本通系列答案
一課一練一本通系列答案 浙江之星學業水平測試系列答案
浙江之星學業水平測試系列答案科目:初中數學 來源: 題型:解答題
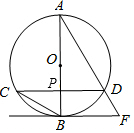 如圖,AB為⊙O的直徑,弦CD⊥AB,垂足為點P,直線BF與AD延長線交于點F,且∠AFB=∠ABC.
如圖,AB為⊙O的直徑,弦CD⊥AB,垂足為點P,直線BF與AD延長線交于點F,且∠AFB=∠ABC.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
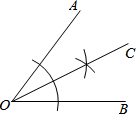 如圖,用直尺和圓規作一個角的平分線,是運用了“全等三角形的對應角相等”這一性質,由作圖所得條件,判定三角形全等運用的方法是( )
如圖,用直尺和圓規作一個角的平分線,是運用了“全等三角形的對應角相等”這一性質,由作圖所得條件,判定三角形全等運用的方法是( )| A. | SSS | B. | ASA | C. | AAS | D. | SAS |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com