
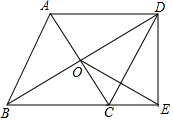
 如圖,菱形ABCD的對角線相交于點O,DE⊥BC的延長線于點E,若菱形的周長為20,AC=6,則線段OE的長是4.
如圖,菱形ABCD的對角線相交于點O,DE⊥BC的延長線于點E,若菱形的周長為20,AC=6,則線段OE的長是4. 分析 先根據菱形的四邊相等得:邊長AD=5,由勾股定理求OD=4,則BD=8,再根據直角三角形斜邊中線等于斜邊一半求OE的長.
解答 解:∵四邊形ABCD是菱形,
∴AC⊥BD,AO=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3,OB=OD,
∵菱形的周長為20,
∴AD=5,
在Rt△AOD中,由勾股定理得:OD=$\sqrt{A{D}^{2}-A{O}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴BD=2OD=8,
∵DE⊥BC,
∴∠DEB=90°,
∵OD=OB,
∴OE=$\frac{1}{2}$BD=$\frac{1}{2}$×8=4,
故答案為:4.
點評 本題考查了菱形的性質、直角三角形斜邊中線的性質、勾股定理,熟練掌握菱形的性質是關鍵:①菱形的四邊相等,根據周長可求邊長;②菱形的對角線互相垂直且平分.


科目:初中數學 來源: 題型:選擇題
| A. | 調查一批汽車的使用壽命 | |
| B. | 調查山東省市民春節期間計劃外出旅游情況 | |
| C. | 調查某航班的旅客是否攜帶了違禁物品 | |
| D. | 調查全國初三學生的視力情況 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y隨x的增大而減小 | B. | 它的圖象與y軸的交點是(0,4) | ||
| C. | 當x<2時,y<0 | D. | 它的圖象不經過第三象限 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 銷售額/萬元 | 14 | 15 | 17 | 19 | 27 | 30 |
| 人數 | 1 | 6 | 3 | 4 | 5 | 1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 若a>b,則ac>bc | B. | 若ac>bc,則a>b | C. | 若a>b,則ac2>bc2 | D. | 若ac2>bc2,則a>b |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
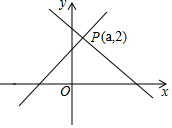 如圖,直線y=x+1與直線y=mx+n相交于點P(a,2),則關于不等式x+1≥mx+n的解集是( )
如圖,直線y=x+1與直線y=mx+n相交于點P(a,2),則關于不等式x+1≥mx+n的解集是( )| A. | x≥-1 | B. | 0≤x≤1 | C. | x≥1 | D. | x≤1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com