
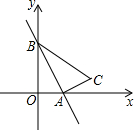
 已知:如圖,一次函數(shù)y=-$\sqrt{3}$x+3的圖象與x軸、y軸分別交于點(diǎn)A、B,以線段AB為直角邊作Rt△ABC,且∠ABC=30°,∠BAC=90°,點(diǎn)C在第一象限
已知:如圖,一次函數(shù)y=-$\sqrt{3}$x+3的圖象與x軸、y軸分別交于點(diǎn)A、B,以線段AB為直角邊作Rt△ABC,且∠ABC=30°,∠BAC=90°,點(diǎn)C在第一象限分析 (1)如圖1中,作CH⊥OA于H.在Rt△ACH中求出CH,AH即可.
(2)①由DE∥AB,可以設(shè)直線DE的解析式為y=-$\sqrt{3}$x+b,把(2$\sqrt{3}$,1)的坐標(biāo)代入得b=7,由此即可解決問題.
②分三種情形討論ⅰ:當(dāng)AP=AB時(shí),如圖2中.ⅱ:當(dāng)BA=BP時(shí),如圖3中,作BT⊥EC于T.ⅲ:當(dāng)PA=PB時(shí),如圖4中,作PH⊥AB于H.分別求解即可.
解答 解:(1)如圖1中,作CH⊥OA于H.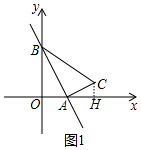
∵一次函數(shù)y=-$\sqrt{3}$x+3的圖象與x軸、y軸分別交于點(diǎn)A、B,
∴A($\sqrt{3}$,0),B(0,3),
∴OA=$\sqrt{3}$,OB=3,
∴AB=$\sqrt{{3}^{2}+(\sqrt{3})^{2}}$=2$\sqrt{3}$,
∴tan∠BAO=$\frac{OB}{OA}$=$\sqrt{3}$,
∴∠BAO=60°,
在Rt△ABC中,∵∠BAC=90°,∠ABC=30°,AB=2$\sqrt{3}$,
∴AC=2,
在Rt△ACH中,∵∠AHC=90°∠CAH=30°,AC=2,
∴CH=1,AH=$\sqrt{3}$,
∴OA=2$\sqrt{3}$,
∴C(2$\sqrt{3}$,1).
(2)①∵DE∥AB,
∴設(shè)直線DE的解析式為y=-$\sqrt{3}$x+b,
把(2$\sqrt{3}$,1)的坐標(biāo)代入得b=7,
∴直線DE的解析式為y=-$\sqrt{3}$x+7.
②應(yīng)分三種情況:
ⅰ:當(dāng)AP=AB時(shí),如圖2中,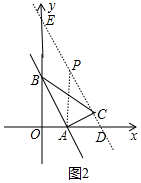
由(1)可知AP=AB=2$\sqrt{3}$,AC=2,
在Rt△APC中,PC=$\sqrt{A{P}^{2}-A{C}^{2}}$=$\sqrt{(2\sqrt{3})^{2}-{2}^{2}}$=2$\sqrt{2}$.
在Rt△ACD中,∵∠ACD=90°,∠CAD=30°,AC=2,
∴CD=$\frac{2\sqrt{3}}{3}$,AD=$\frac{4\sqrt{3}}{3}$,
在Rt△EOD中,∵∠OED=30°,OD=$\frac{7\sqrt{3}}{3}$,
∴DE=2OD=$\frac{14\sqrt{3}}{3}$,
∴EC=ED-CD=$\frac{14\sqrt{3}}{3}$-$\frac{2\sqrt{3}}{3}$=4$\sqrt{3}$,
∴EP=EC-PC=4$\sqrt{3}$-2$\sqrt{2}$
ⅱ:當(dāng)BA=BP時(shí),如圖3中,作BT⊥EC于T,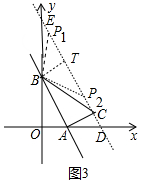
∵BT=AC=2,ET=TC=2$\sqrt{3}$,
TP1=TP2=$\sqrt{(2\sqrt{3})^{2}-{2}^{2}}$=2$\sqrt{2}$,
∴EP1=2$\sqrt{3}$-2$\sqrt{2}$,EP2=2$\sqrt{3}$+2$\sqrt{2}$.
ⅲ:當(dāng)PA=PB時(shí),如圖4中,作PH⊥AB于H.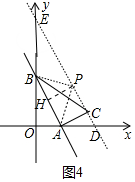
∴BH=AH=PC=$\sqrt{3}$,
∴EP=EC-PC=4$\sqrt{3}$-$\sqrt{3}$=3$\sqrt{3}$.
點(diǎn)評(píng) 本題考查一次函數(shù)的應(yīng)用、待定系數(shù)法、等腰三角形的判定和性質(zhì)、兩直線平行k相同、勾股定理、直角三角形30度角性質(zhì)等知識(shí),解題的關(guān)鍵是靈活運(yùn)用所學(xué)知識(shí)解決問題,學(xué)會(huì)用分類討論的思想思考問題,屬于中考?jí)狠S題.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,四邊形ABCD中DC∥AB,將四邊形沿對(duì)角線AC折疊,使點(diǎn)B落在點(diǎn)B′處,若∠1=∠2=44°,則∠B為( )
如圖,四邊形ABCD中DC∥AB,將四邊形沿對(duì)角線AC折疊,使點(diǎn)B落在點(diǎn)B′處,若∠1=∠2=44°,則∠B為( )| A. | 66° | B. | 104° | C. | 114° | D. | 124° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2個(gè) | B. | 3個(gè) | C. | 4個(gè) | D. | 5個(gè) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
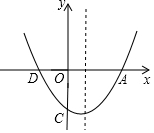 如圖,已知拋物線的頂點(diǎn)為(1,-$\frac{27}{8}$),與y軸交點(diǎn)C(0,-3),與x軸的交點(diǎn)為A,D(A在D的右側(cè)).
如圖,已知拋物線的頂點(diǎn)為(1,-$\frac{27}{8}$),與y軸交點(diǎn)C(0,-3),與x軸的交點(diǎn)為A,D(A在D的右側(cè)).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
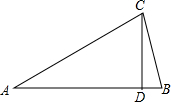 如圖,在∠A=30°的等腰三角形ABC中,AB=AC,若過點(diǎn)C作CD⊥AB于點(diǎn)D,則∠BCD=15°.根據(jù)圖形,計(jì)算tan15°的值.
如圖,在∠A=30°的等腰三角形ABC中,AB=AC,若過點(diǎn)C作CD⊥AB于點(diǎn)D,則∠BCD=15°.根據(jù)圖形,計(jì)算tan15°的值.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com