Question

4．有一副直角三角板，在三角板ABC中，∠BAC=90°，AB=AC=6，在三角板DEF中，∠FDE=90°，DF=4，DE=4$\sqrt{3}$，將這副直角三角板按如圖（1）所示位置擺放，點B與點F重合，直角邊BA與FD在同一條直線上．現固定三角板ABC，將三角板DEF沿射線BA方向平行移動，當點F運動到點A時停止運動．
（1）如圖（2），當三角板DEF運動到點D與點A重合時，設EF與BC交于點M，則∠EMC=15度；
（2）如圖（3），在三角板DEF運動過程中，當EF經過點C時，求FC的長；
（3）在三角板DEF運動過程中，當D在BA的延長線上時，設BF=x，兩塊三角板重疊部分的面積為y．求y與x的函數關系式，并求出對應的x取值范圍．

Answer 1

分析 （1）如題圖2所示，由三角形的外角性質可得∠EMC=∠FMB=∠DFE-∠ABC；
（2）如題圖3所示，在Rt△ACF中，解直角三角形即可得出FC的長；
（3）認真分析三角板的運動過程，明確不同時段重疊圖形的變化情況：（I）當0≤x≤2時，如答圖1所示；（II）當2＜x≤6-2$\sqrt{3}$時，如答圖2所示；（III）當6-2$\sqrt{3}$＜x≤6時，如答圖3所示．

解答 解：（1）如題圖2所示，∵在三角板DEF中，∠FDE=90°，DF=4，DE=4$\sqrt{3}$，
∴tan∠DFE=$\frac{DE}{DF}$=$\sqrt{3}$，
∴∠DFE=60°，
∴∠EMC=∠FMB=∠DFE-∠ABC=60°-45°=15°；
故答案為：15°；

（2）如題圖3所示，當EF經過點C時，
FC=$\frac{AC}{sin∠AFC}$=$\frac{6}{sin60°}$=$\frac{6}{\frac{\sqrt{3}}{2}}$=4$\sqrt{3}$；

（3）在三角板DEF運動過程中，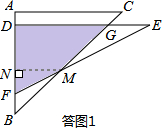
（I）當0≤x≤2時，如答圖1所示，設DE交BC于點G．
過點M作MN⊥AB于點N，則△MNB為等腰直角三角形，MN=BN．
又∵NF=$\frac{MN}{tan60°}$=$\frac{\sqrt{3}}{3}$MN，BN=NF+BF，
∴NF+BF=MN，即$\frac{\sqrt{3}}{3}$MN+x=MN，
解得：MN=$\frac{3+\sqrt{3}}{2}x$．
y=S_△BDG-S_△BFM
=$\frac{1}{2}$BD•DG-$\frac{1}{2}$BF•MN
=$\frac{1}{2}$（x+4）²-$\frac{1}{2}$x•$\frac{3+\sqrt{3}}{2}$x
=-$\frac{\sqrt{3}+1}{4}$x²+4x+8；

（II）當2＜x≤6-2$\sqrt{3}$時，如答圖2所示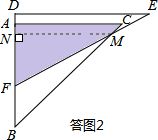，過點M作MN⊥AB于點N，則△MNB為等腰直角三角形，MN=BN．
又∵NF=$\frac{MN}{tan60°}$=$\frac{\sqrt{3}}{3}$MN，BN=NF+BF，
∴NF+BF=MN，即$\frac{\sqrt{3}}{3}$MN+x=MN，
解得：MN=$\frac{3+\sqrt{3}}{2}$x．
y=S_△ABC-S_△BFM
=$\frac{1}{2}$AB•AC-$\frac{1}{2}$BF•MN
=$\frac{1}{2}$×6²-$\frac{1}{2}$x•$\frac{3+\sqrt{3}}{2}$x
=-$\frac{3+\sqrt{3}}{4}$x²+18；

（III）當6-2$\sqrt{3}$＜x≤6時，如答圖3所示，設BF=x，則AF=AB-BF=6-x，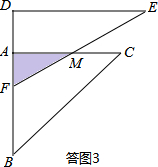
設AC與EF交于點M，則AM=AF•tan60°=$\sqrt{3}$（6-x）．
y=S_△AFM=$\frac{1}{2}$AF•AM=$\frac{1}{2}$（6-x）•$\sqrt{3}$（6-x）=$\frac{\sqrt{3}}{2}$x²-6$\sqrt{3}$x+18$\sqrt{3}$．
綜上所述，y與x的函數解析式為：
y=$\left\{\begin{array}{l}{-\frac{\sqrt{3}+1}{4}{x}^{2}+4x+8（0≤x≤2）}\\{-\frac{3+\sqrt{3}}{4}{x}^{2}+18（2＜x≤6-2\sqrt{3}）}\\{\frac{\sqrt{3}}{2}{x}^{2}-6\sqrt{3}x+18（6-2\sqrt{3}＜x≤6）}\end{array}\right.$．

點評 本題屬于三角形綜合題，解題的關鍵是認真分析三角板的運動過程，明確不同時段重疊圖形形狀的變化情況．在解題計算過程中，除利用三角函數進行計算外，也可以利用三角形相似，殊途同歸．解題時注意分類討論思想的運用．