Question

8．定義：若一次函數y=ax+b與反比例函數y=-$\frac{c}{x}$滿足$\frac{a}{b}=\frac{b}{c}$，則稱y=ax²+bx+c為一次函數和反比例函數的“等比”函數．
（1）試判斷（需寫出判斷過程）一次函數y=x+b與反比例函數y=-$\frac{9}{x}$是否存在“等比”函數？若存在，請寫出它們的“等比”函數的解析式；
（2）若一次函數y=9x+b（b＜0）與反比例函數y=-$\frac{c}{x}$存在“等比”函數，且“等比”函數的圖象與y=-$\frac{c}{x}$的圖象的交點的橫坐標為x=-$\frac{1}{3}$，求反比例函數的解析式；
（3）若一次函數y=ax+b與反比例函數y=-$\frac{c}{x}$（其中a＞0，c＞0，a=3b）存在“等比”函數，且y=ax+b的圖象與“等比”函數圖象有兩個交點A（x₁，y₁）、B（x₂，y₂），試判斷“等比”函數圖象上是否存在一點P（x，y）（其中x₁＜x＜x₂），使得△ABP的面積最大？若存在，請用c表示△ABP面積的最大值；若不存在，請說明理由．

Answer 1

分析 （1）假設存在，根據等比函數定義得出b²=9，繼而可得b的值，從而得出解析式；
（2）根據等比函數定義及b＜0得出b²=9c，即b=-3 $\sqrt{c}$，根據“等比”函數的圖象與y=-$\frac{c}{x}$的圖象的交點的橫坐標為x=-$\frac{1}{3}$，列出方程即可解決問題．
（3）存在，由題意b²=ac，且a=3b，推出b²=3bc，因為a＞0，c＞0，所以b=3c，a=9c，則一次函數解析式為y=9cx+3c，“等比”函數解析式為y=9cx²+3cx+c，即9x²-6x-2=0，可得x₁+x₂=$\frac{2}{3}$，x₁x₂=-$\frac{2}{9}$，|x₁-x₂|=$\sqrt{（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{（\frac{2}{3}）^{2}-4×（-\frac{2}{9}）}$=$\frac{2}{3}$$\sqrt{3}$，再構建二次函數，利用二次函數的性質即可解決問題．

解答 解：（1）存在，
假設一次函數y=x+b與反比例函數y=-$\frac{9}{x}$存在“等比”函數，則b²=9，
解得：b=3或-3，
∴存在“等比”函數，其解析式為y=x²+3x+9或y=x²-3x+9；

（2）根據題意知，b²=9c，
∴b=±3 $\sqrt{c}$，
∵b＜0，
∴b=-3 $\sqrt{c}$，
則“等比”函數的解析式為y=9x²-3 $\sqrt{c}$x+c，
根據題意，x=-$\frac{1}{3}$時，9x²-3 $\sqrt{c}$x+c=-$\frac{c}{x}$，
∴1+$\sqrt{c}$+c=3c，即（ $\sqrt{c}$-1）（2 $\sqrt{c}$+1）=0，
解得：$\sqrt{c}$=1，
∴c=1，
故反比例函數的解析式為y=-$\frac{1}{x}$；

（3）存在，
∵b²=ac，且a=3b，
∴b²=3bc，
∵a＞0，c＞0，
∴b=3c，a=9c，
則一次函數解析式為y=9cx+3c，“等比”函數解析式為y=9cx²+3cx+c，
由9cx²+3cx+c=9cx+3c化簡得：9x²-6x-2=0，
∴x₁+x₂=$\frac{2}{3}$，x₁x₂=-$\frac{2}{9}$，
∴|x₁-x₂|=$\sqrt{（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{（\frac{2}{3}）^{2}-4×（-\frac{2}{9}）}$=$\frac{2}{3}$$\sqrt{3}$，
如圖，過點P作PH⊥x軸，交AB于H，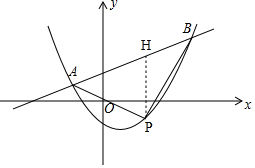

∴H（x，9cx+3c）、P（x，9cx²+3cx+c），
∴PH=9cx+3c-（9cx²+3cx+c）=-c（9x²-6x-2），
∴S=$\frac{1}{2}$PH•|x₁-x₂|=-$\frac{\sqrt{3}}{3}$c（9x²-6x-2）=-3$\sqrt{3}$c（x-$\frac{1}{3}$）²+$\sqrt{3}$c，
∴當x=$\frac{1}{3}$時，S取得最大值，最大值為 $\sqrt{3}$c．

點評 本題考查二次函數綜合題、一次函數的應用、一元二次方程的根與系數的關系等知識，解題的關鍵是理解新定義，學會利用方程組解決兩個函數圖象的交點問題，學會構建二次函數利用二次函數的性質解決最值問題，屬于中考壓軸題．