
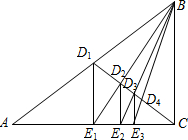
 如圖,已知Rt△ABC的面積為1,D1是斜邊AB的中點,過D1作D1E1⊥AC于E1,連接BE1交CD1于D2;過D2作D2E2⊥AC于E2,連接BE2交CD1于D3;過D3作D3E3⊥AC于E3,…,如此繼續,可以依次得到點D4,D5,…,Dn,分別記△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面積為S1,S2,S3,…Sn.則Sn等于( )
如圖,已知Rt△ABC的面積為1,D1是斜邊AB的中點,過D1作D1E1⊥AC于E1,連接BE1交CD1于D2;過D2作D2E2⊥AC于E2,連接BE2交CD1于D3;過D3作D3E3⊥AC于E3,…,如此繼續,可以依次得到點D4,D5,…,Dn,分別記△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面積為S1,S2,S3,…Sn.則Sn等于( )| A. | $\frac{1}{(n+1)^{2}}$ | B. | $\frac{1}{(2n)^{2}}$ | C. | $\frac{1}{4n}$ | D. | $\frac{1}{{2}^{n+1}}$ |
分析 根據直角三角形的性質以及相似三角形的性質解答即可.
解答 解:由題意得:D1E1∥BC,∴△BD1E1與△CD1E1同底同高,面積相等,以此類推;
根據直角三角形的性質以及相似三角形的性質可知:D1E1=$\frac{1}{2}$BC,CE1=$\frac{1}{2}$AC,S1=$\frac{1}{2}$S△ABC;
∴在△ACB中,D2為其重心,
∴D2E1=$\frac{1}{3}$BE1,
∴D2E2=$\frac{1}{3}$BC,CE2=$\frac{1}{3}$AC,S2=$\frac{1}{{3}^{2}}$S△ABC,
∵D2E2:D1E1=2:3,D1E1:BC=1:2,
∴BC:D2E2=2D1E1:$\frac{2}{3}$D1E1=3,
∴CD3:CD2=D3E3:D2E2=CE3:CE2=3:4,
∴D3E3=$\frac{3}{4}$D2E2=$\frac{3}{4}$×$\frac{1}{3}$BC=$\frac{1}{4}$BC,CE3=$\frac{3}{4}$CE2=$\frac{3}{4}$×$\frac{1}{3}$AC=$\frac{1}{4}$AC,S3=$\frac{1}{{4}^{2}}$S△ABC…;
∴Sn=$\frac{1}{(n+1)^{2}}$S△ABC=$\frac{1}{(n+1)^{2}}$;
故選:A.
點評 本題考查了相似三角形的判定與性質,解決本題的關鍵是據直角三角形的性質以及相似三角形的性質得到第一個三角形的面積與原三角形的面積的規律.也考查了重心的性質即三角形三邊中線的交點到頂點的距離等于它到對邊中點距離的兩倍.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:選擇題
| A. | 面積為8的正方形邊長是$\sqrt{8}$ | B. | $\sqrt{8}$是無理數 | ||
| C. | 在數軸上沒有對應$\sqrt{8}$的點 | D. | $\sqrt{8}$介于整數2和3之間 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
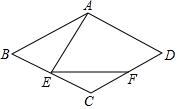 如圖,四邊形ABCD為菱形,∠C=120°,點E是BC上一點.∠AEF=60°,EF交CD于F,求證:(1)∠BAE=∠CEF;(2)AE=EF.
如圖,四邊形ABCD為菱形,∠C=120°,點E是BC上一點.∠AEF=60°,EF交CD于F,求證:(1)∠BAE=∠CEF;(2)AE=EF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
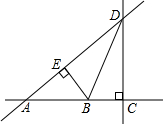 如圖所示,直線AD與直線BD相交于點D,BE⊥AD垂足為點E,點B到直線AD的距離是線段BE的長度,點D到直線AB的距離是線段DC的長度.
如圖所示,直線AD與直線BD相交于點D,BE⊥AD垂足為點E,點B到直線AD的距離是線段BE的長度,點D到直線AB的距離是線段DC的長度.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com