
分析 利用絕對值三角不等式求得|x|+|x-2|≥2,結合題意可得 2≥m,從而求得m的最大值.
解答 解:根據題意得:|x|+$\sqrt{x-1}$+|x-2|≥m,
∵$\sqrt{x-1}$≥0,
∴x-1≥0,
∴x≥1,
當1≤x≤2時,|x|+|x-2|的最小值為2,
∵$\sqrt{x-1}$≥0,
∴當x=1時,|x|+$\sqrt{x-1}$+|x-2的最小值為2,
∴2≥m,
∴m可取得的最大值為2;
故答案為:2.
點評 本題主要考查有理數無理數的概念與運算、絕對值以及不等式,函數的恒成立問題;解題的關鍵是要注意函數的恒成立與函數的最值的相互轉化,體現了轉化思想在解題中的應用解題中要注意函數定義域的條件.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:選擇題
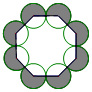 如圖,把八個等圓按相鄰兩兩外切擺放,其圓心連線構成一個正八邊形,設正八邊形內側八個扇形(無陰影部分)面積之和為S1,正八邊形外側八個扇形(有陰影部分)面積之和為S2,則$\frac{{S}_{1}}{{S}_{2}}$=( )
如圖,把八個等圓按相鄰兩兩外切擺放,其圓心連線構成一個正八邊形,設正八邊形內側八個扇形(無陰影部分)面積之和為S1,正八邊形外側八個扇形(有陰影部分)面積之和為S2,則$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
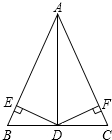 如圖,在△ABC中,AD是△ABC中的角平分線,BD=CD,DE⊥AB,DF⊥AC,請你在圖中找出三對全等的三角形,并任選一對進行證明.
如圖,在△ABC中,AD是△ABC中的角平分線,BD=CD,DE⊥AB,DF⊥AC,請你在圖中找出三對全等的三角形,并任選一對進行證明.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com