
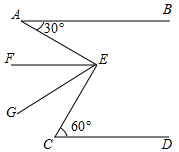
 如圖,AB∥CD,∠BAE=30°,∠ECD=60°,EF、EG等分∠AEC,試判斷EF與AB的關系并寫出你的理由.
如圖,AB∥CD,∠BAE=30°,∠ECD=60°,EF、EG等分∠AEC,試判斷EF與AB的關系并寫出你的理由. 分析 先延長CE交AB于H,根據平行線的性質,得出∠AHE=60°,再根據三角形外角性質,得出∠AEC=∠A+∠AHE=90°,根據EF、EG等分∠AEC,得到∠AEF=$\frac{1}{3}$∠AEC=30°,最后根據∠A=∠AEF,即可判定AB∥EF.
解答 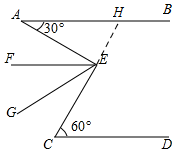 解:EF與AB互相平行.
解:EF與AB互相平行.
理由:延長CE交AB于H,
∵AB∥CD,
∴∠C=∠AHE=60°,
∵∠AEC是△AEH的外角,
∴∠AEC=∠A+∠AHE=30°+60°=90°,
又∵EF、EG等分∠AEC,
∴∠AEF=$\frac{1}{3}$∠AEC=30°,
∴∠A=∠AEF,
∴AB∥EF.
點評 本題主要考查了平行線的判定與性質的綜合應用,解題時注意:兩直線平行,內錯角相等;內錯角相等,兩直線平行.解決問題的關鍵是作輔助線,根據三角形外角性質求得∠AEC的度數.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
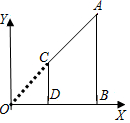 如圖,AB,CD都垂直于x軸,垂足分別為B,D,若A(6,3),C(2,1),
如圖,AB,CD都垂直于x軸,垂足分別為B,D,若A(6,3),C(2,1),| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:8 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
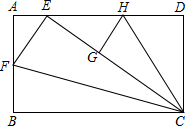 如圖矩形ABCD是一張標準紙,長BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF對折使點B恰好落在邊AD上的點E處,再把△DCH沿CH對折使點D落在線段CE上的點G處.
如圖矩形ABCD是一張標準紙,長BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF對折使點B恰好落在邊AD上的點E處,再把△DCH沿CH對折使點D落在線段CE上的點G處.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,點A,B,C都在格點上,請按要求回答問題或畫圖:
如圖,點A,B,C都在格點上,請按要求回答問題或畫圖:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 同旁內角互補 | |
| B. | 一個角的補角大于這個角 | |
| C. | 同位角不相等,兩直線不平行 | |
| D. | 如果兩個角不相等,那么這兩個角不是對頂角 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| 16進制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 10進制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| A. | 1C | B. | 1A | C. | 19 | D. | 21 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com