
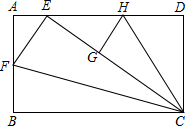
 如圖矩形ABCD是一張標準紙,長BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF對折使點B恰好落在邊AD上的點E處,再把△DCH沿CH對折使點D落在線段CE上的點G處.
如圖矩形ABCD是一張標準紙,長BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF對折使點B恰好落在邊AD上的點E處,再把△DCH沿CH對折使點D落在線段CE上的點G處.分析 根據折疊的性質得到CE=CB=$\sqrt{2}$,CG=CD=1,∠FEC=∠B=90°,∠HGC=∠HGE=∠D=90°,求得CE=$\sqrt{2}$CD,∠HGE=∠A=90°,根據三角函數的定義得到△EC是等腰直角三角形,得到AE=EG,根據全等三角形的判定定理即可得到結論;
(2)根據等腰直角三角形的性質得到EG=HG=DH=$\sqrt{2}$-1,根據三角函數的定義即可得到結論.
解答 解:(1)∵BC=AD=$\sqrt{2}$,AB=CD=1,
∵把△BCF沿CF對折使點B恰好落在邊AD上的點E處,再把△DCH沿CH對折使點D落在線段CE上的點G處,
∴CE=CB=$\sqrt{2}$,CG=CD=1,∠FEC=∠B=90°,∠HGC=∠HGE=∠D=90°,
∴CE=$\sqrt{2}$CD,∠HGE=∠A=90°,
∴tan∠DEC=$\frac{CD}{EC}=\frac{\sqrt{2}}{2}$,EG=EC-GC=$\sqrt{2}$-1,
∴∠DEC=45°,
∴△DEC是等腰直角三角形,
∴∠AEF=45°,
∴DE=DC,∠AEF=∠DEC,
∴AE=AD-DE=$\sqrt{2}$-1,
∴AE=EG,
在△AEF與△GHE中,$\left\{\begin{array}{l}{∠A=∠EGH}\\{AE=EG}\\{∠AEF=∠GEH}\end{array}\right.$,
∴△AEF≌△GHE;
(2)由(1)知∠DCH=∠GCH=$\frac{1}{2}×$45°=2.5°,DH=GH,△HEG是等腰直角三角形,
∴EG=HG=DH=$\sqrt{2}$-1,
∴tan∠DCH=tan22.5°=$\frac{DH}{CD}$=$\sqrt{2}$-1.
點評 本題考查了翻折變換(折疊問題),全等三角形的判定和性質,等腰直角三角形的判定和性質,三角函數的定義,熟練掌握折疊的性質是解題的關鍵.


 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:初中數學 來源: 題型:選擇題
| A. | x≥-2且x≠0 | B. | x>0 | C. | -2≤x<0 | D. | 0<x≤2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
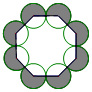 如圖,把八個等圓按相鄰兩兩外切擺放,其圓心連線構成一個正八邊形,設正八邊形內側八個扇形(無陰影部分)面積之和為S1,正八邊形外側八個扇形(有陰影部分)面積之和為S2,則$\frac{{S}_{1}}{{S}_{2}}$=( )
如圖,把八個等圓按相鄰兩兩外切擺放,其圓心連線構成一個正八邊形,設正八邊形內側八個扇形(無陰影部分)面積之和為S1,正八邊形外側八個扇形(有陰影部分)面積之和為S2,則$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
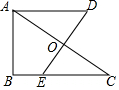 如圖,Rt△ABC,∠B=90°,AC的垂直平分線交BC于點E,垂足為點O,過點A作BC的平行線,與直線OE交于點D,若AB=4,BC=6,則AD的長為$\frac{13}{3}$.
如圖,Rt△ABC,∠B=90°,AC的垂直平分線交BC于點E,垂足為點O,過點A作BC的平行線,與直線OE交于點D,若AB=4,BC=6,則AD的長為$\frac{13}{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
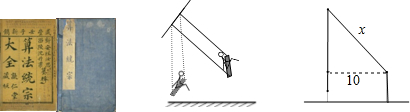
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com