
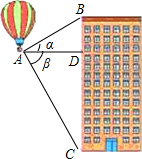
 如圖,熱氣球探測器顯示,從熱氣球A處看一棟樓頂部B處的仰角為30°,看這棟樓底部C處的俯角為60°,熱氣球與樓的水平距離AD為100米,試求這棟樓的高度BC.
如圖,熱氣球探測器顯示,從熱氣球A處看一棟樓頂部B處的仰角為30°,看這棟樓底部C處的俯角為60°,熱氣球與樓的水平距離AD為100米,試求這棟樓的高度BC. 分析 在直角三角形ADB中和直角三角形ACD中,根據銳角三角函數中的正切可以分別求得BD和CD的長,從而可以求得BC的長,本題得以解決.
解答 解:由題意可得,
α=30°,β=60°,AD=100米,∠ADC=∠ADB=90°,
∴在Rt△ADB中,α=30°,AD=100米,
∴tanα=$\frac{BD}{AD}$=$\frac{BD}{100}$=$\frac{\sqrt{3}}{3}$,
∴BD=$\frac{100\sqrt{3}}{3}$米,
在Rt△ADC中,β=60°,AD=100米,
∴tanβ=$\frac{CD}{AD}=\frac{CD}{100}=\sqrt{3}$,
∴CD=100$\sqrt{3}$米,
∴BC=BD+CD=$\frac{100\sqrt{3}}{3}+100\sqrt{3}=\frac{400\sqrt{3}}{3}$米,
即這棟樓的高度BC是$\frac{400\sqrt{3}}{3}$米.
點評 本題考查解直角三角形的應用-仰角俯角問題、銳角三角函數,解答此類問題的關鍵是明確題意,利用銳角三角函數解答.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
 某企業生產并銷售某種產品,假設銷售量與產量相等,圖中的折線ABD、線段CD分別表示該產品每千克生產成本y1(元)、銷售價y2(單位:元)與產量x(單位:kg)之間的函數關系.
某企業生產并銷售某種產品,假設銷售量與產量相等,圖中的折線ABD、線段CD分別表示該產品每千克生產成本y1(元)、銷售價y2(單位:元)與產量x(單位:kg)之間的函數關系.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖所示,已知△ABC中,∠BAC=90°,AB=AC,MN是經過點A的直線,BD⊥MN,CE⊥MN,垂足分別為點D、E.
如圖所示,已知△ABC中,∠BAC=90°,AB=AC,MN是經過點A的直線,BD⊥MN,CE⊥MN,垂足分別為點D、E.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
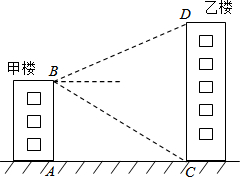 如圖,甲、乙兩樓的距離AC=30m,甲樓高AB=40m,自甲樓樓頂的B處看乙樓樓頂的D處,仰角為28°,求乙樓的高CD的長.(結果精確到0.1m,參考數據:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
如圖,甲、乙兩樓的距離AC=30m,甲樓高AB=40m,自甲樓樓頂的B處看乙樓樓頂的D處,仰角為28°,求乙樓的高CD的長.(結果精確到0.1m,參考數據:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com