
分析 畫出示意圖,利用勾股定理表示出兩車的距離,然后利用配方法求出兩車的距離最小值,計算出汽車行走路程與120km比較,可判斷是否已過交叉口.
解答 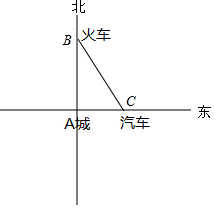 解:如圖所示:
解:如圖所示:
設兩車經過時間為t,兩車之間的距離為y,兩車的行駛方向如圖所示,由題意得
AB=240-120t,AC=120-120t,
在Rt△ABC中,BC2=AB2+AC2=(240-120t)2+(120-120t)2=28800(t-$\frac{3}{2}$)2+7200,
當t=$\frac{3}{2}$時,BC之間的距離最小,此時BC=$\sqrt{7200}$=60$\sqrt{2}$km,
當t=$\frac{3}{2}$h時,汽車運動的距離為120×$\frac{3}{2}$=180km>120km,
故已過鐵路與公路的交叉口.
答:當經過$\frac{3}{2}$小時時汽車與火車的距離最近,此時汽車已過鐵路與公路的交叉口.
點評 本題考查了二次函數的應用、勾股定理的知識,解答本題的關鍵是表示出兩車之間的距離表達式,注意掌握配方法求二次函數最值得應用,難度較大.


科目:初中數學 來源: 題型:選擇題
| A. | $\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}-xy}$ | B. | $\frac{x+1}{{x}^{2}-1}$ | ||
| C. | $\frac{{x}^{2}-1}{{x}^{2}+1}$ | D. | $\frac{{x}^{2}-36}{2x+12}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在△ABC中,AB=AC,BD和CE是兩腰上的高,交于點O,連接AO并延長交BC于點F.則圖中全等三角形的對數是( )
如圖,在△ABC中,AB=AC,BD和CE是兩腰上的高,交于點O,連接AO并延長交BC于點F.則圖中全等三角形的對數是( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{2}{x-2}$ | B. | $\frac{2}{4x}$ | C. | $\frac{y-x}{{x}^{2}-{y}^{2}}$ | D. | $\frac{{x}^{2}-4x+4}{x-2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
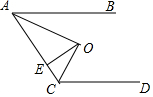 如圖所示,AB∥CD,O為∠BAC、∠ACD的平分線交點,OE⊥AC于E,若OE=2,則AB與CD之間的距離是( )
如圖所示,AB∥CD,O為∠BAC、∠ACD的平分線交點,OE⊥AC于E,若OE=2,則AB與CD之間的距離是( )| A. | 2 | B. | 4 | C. | 8 | D. | 無法確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com