
 如圖,在△ABC中,AB=AC,BD和CE是兩腰上的高,交于點O,連接AO并延長交BC于點F.則圖中全等三角形的對數是( )
如圖,在△ABC中,AB=AC,BD和CE是兩腰上的高,交于點O,連接AO并延長交BC于點F.則圖中全等三角形的對數是( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 ①△BDC≌△CEB,根據等邊對等角得:∠ABC=∠ACB,由高得:∠BDC=∠CEB=90°,所以利用AAS可證明全等;
②△BEO≌△CDO,加上對頂角相等,利用AAS可證明全等;
③△AEO≌△ADO,根據HL可證明全等;
④△ABF≌△ACF,根據SAS可證明全等;
⑤△BOF≌△COF,根據等腰三角形三線合一的性質得:BF=FC,∠AFB=∠AFC,利用SAS可證明全等;
⑥△AOB≌△AOC,根據SAS可證明全等;
⑦△ABD≌△ACE,利用AAS可證明全等.
解答 解:有7對全等三角形:
①△BDC≌△CEB,理由是:
∵AB=AC,
∴∠ABC=∠ACB,
∵BD和CE是兩腰上的高,
∴∠BDC=∠CEB=90°,
在△BDC和△CEB中,
∵$\left\{\begin{array}{l}{∠BDC=∠CEB}\\{∠ACB=∠ABC}\\{BC=CB}\end{array}\right.$,
∴△BDC≌△CEB(AAS),
∴BE=DC,
②△BEO≌△CDO,理由是:
在△BEO和△CDO中,
∵$\left\{\begin{array}{l}{∠BEO=∠CDO}\\{∠BOE=∠COD}\\{BE=CD}\end{array}\right.$,
∴△BEO≌△CDO(AAS),
③△AEO≌△ADO,理由是:
由△BEO≌△CDO得:EO=DO,
在Rt△AEO和Rt△ADO中,
$\left\{\begin{array}{l}{AO=AO}\\{EO=OD}\end{array}\right.$,
∴Rt△AEO≌Rt△ADO(HL),
∴∠EAO=∠DAO,
④△ABF≌△ACF,理由是:
在△ABF和△ACF中,
∵$\left\{\begin{array}{l}{AB=AC}\\{∠EAO=∠DAO}\\{AF=AF}\end{array}\right.$,
∴△ABF≌△ACF(SAS),
⑤△BOF≌△COF,理由是:
∵AB=AC,∠BAF=∠CAF,
∴BF=FC,∠AFB=∠AFC,
在△BOF和△COF中,
∵$\left\{\begin{array}{l}{OF=OF}\\{∠AFB=∠ADC}\\{BF=FC}\end{array}\right.$,
∴△BOF≌△COF(SAS),
⑥△AOB≌△AOC,理由是:
在△AOB和△AOC中,
∵$\left\{\begin{array}{l}{AB=AC}\\{∠BAO=∠CAO}\\{AO=AO}\end{array}\right.$,
∴△AOB≌△AOC(SAS),
⑦△ABD≌△ACE,理由是:
在△ABD和△ACE中,
∵$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{∠ADB=∠AEC=90°}\end{array}\right.$,
∴△ABD≌△ACE(AAS);
故選C.
點評 本題主要考查了三角形全等的性質和判定、等腰三角形的性質,熟練掌握三角形全等的判定方法是關鍵,要書寫三角形全等時要按順序書寫,才能做到不重不漏.


 ABC考王全優卷系列答案
ABC考王全優卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | $\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=1\\ y=4\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=4\\ y=1\end{array}\right.$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
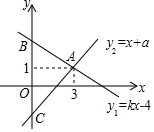 如圖,一次函數y1=kx+4與y2=x+a的圖象相交于點A(3,1),與y軸分別相交于點B、C兩點.
如圖,一次函數y1=kx+4與y2=x+a的圖象相交于點A(3,1),與y軸分別相交于點B、C兩點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com