
 如圖,AA′,BB′,CC′相交于點O,且A′B′∥AB,B′C′∥BC,A′C′∥AC,OB=3OB′,判斷△ABC的面積與△A′B′C′的面積有什么關系?
如圖,AA′,BB′,CC′相交于點O,且A′B′∥AB,B′C′∥BC,A′C′∥AC,OB=3OB′,判斷△ABC的面積與△A′B′C′的面積有什么關系? 分析 結論:S△ABC=9•S△A′B′C′.只要證明$\frac{A′B′}{AB}$=$\frac{B′C′}{BC}$=$\frac{A′C′}{AC}$=$\frac{1}{3}$,推出△ABC∽△A′B′C′,推出$\frac{{S}_{△A′B′C′}}{{S}_{△ABC}}$=($\frac{1}{3}$)2=$\frac{1}{9}$,即可證明.
解答 解:S△ABC=9•S△A′B′C′.
理由: ∵A′B′∥AB,B′C′∥BC,A′C′∥AC,OB=3OB′,
∵A′B′∥AB,B′C′∥BC,A′C′∥AC,OB=3OB′,
∴$\frac{A′B′}{AB}$=$\frac{OA′}{OA}$=$\frac{OB′}{OB}$=$\frac{1}{3}$,$\frac{B′C′}{BC}$=$\frac{OB′}{OB}$,$\frac{A′C′}{AC}$=$\frac{OA′}{OA}$,
∴$\frac{A′B′}{AB}$=$\frac{B′C′}{BC}$=$\frac{A′C′}{AC}$=$\frac{1}{3}$,
∴△ABC∽△A′B′C′,
∴$\frac{{S}_{△A′B′C′}}{{S}_{△ABC}}$=($\frac{1}{3}$)2=$\frac{1}{9}$,
∴S△ABC=9•S△A′B′C′.
點評 本題考查相似三角形的判定和性質、平行線分線段成比例定理等知識,解題的關鍵是熟練掌握相似三角形的判定和性質,屬于中考常考題型.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
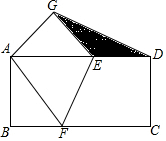 如圖,把長方形紙片ABCD折疊,使其對角頂點C與A重合.若長方形的長BC為8,寬AB為4,則折痕EF的長度為( )
如圖,把長方形紙片ABCD折疊,使其對角頂點C與A重合.若長方形的長BC為8,寬AB為4,則折痕EF的長度為( )| A. | 5 | B. | 3$\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
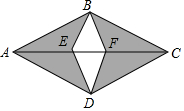 如圖是某房間木地板的一個圖案,其中AB=BC=CD=DA,BE=DE=DF=FB,圖案由有花紋的全等三角形木塊(陰影部分)和無花紋的全等三角形木塊(中間部分)拼成,這個圖案的面積是0.05m2.若房間的面積是23m2,問最少需要有花紋的三角形木塊和無花紋的木塊各多少塊?
如圖是某房間木地板的一個圖案,其中AB=BC=CD=DA,BE=DE=DF=FB,圖案由有花紋的全等三角形木塊(陰影部分)和無花紋的全等三角形木塊(中間部分)拼成,這個圖案的面積是0.05m2.若房間的面積是23m2,問最少需要有花紋的三角形木塊和無花紋的木塊各多少塊?查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | ±$\sqrt{6}$ | B. | 4 | C. | ±$\sqrt{6}$或4 | D. | 4或-$\sqrt{6}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
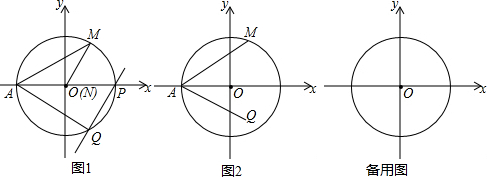
 如圖,在平面直角坐標系中.O為坐標原點,直線y=-$\frac{3}{4}$x+3與x軸、y軸分別交于A,B兩點.點P從點A出發,以每秒1個單位的速度沿射線AO勻速運動,設點P的運動時間為t秒.過點P與直線AB垂直的直線與y軸交于點E.
如圖,在平面直角坐標系中.O為坐標原點,直線y=-$\frac{3}{4}$x+3與x軸、y軸分別交于A,B兩點.點P從點A出發,以每秒1個單位的速度沿射線AO勻速運動,設點P的運動時間為t秒.過點P與直線AB垂直的直線與y軸交于點E.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com