
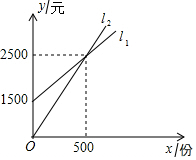
 某公司要印制產品宣傳材料,l1反映了甲印刷廠的收費y1(元)與印制數量x(份)間的關系,l2反映了乙印刷廠的收費y2(元)與印制數量x(份)間的關系.
某公司要印制產品宣傳材料,l1反映了甲印刷廠的收費y1(元)與印制數量x(份)間的關系,l2反映了乙印刷廠的收費y2(元)與印制數量x(份)間的關系.分析 (1)觀察圖象,即可判斷.
(2)利用待定系數法即可解決問題.
(3)當y=4000時,分別求出自變量的取值即可判斷.
解答 解:(1)由圖象可知,當印制500份時,甲、乙印刷廠的收費相同.
(2)設l1的解析式為y=kx+b,
∵經過點(0,1500),(500,2500),
∴$\left\{\begin{array}{l}{b=1500}\\{500k+b=2500}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{b=1500}\end{array}\right.$,
∴l1的解析式為y=2x+1500,
設l2的解析式為y=k′x,則有500k′=2500,
∴k′=5,
∴l2的解析式為y=5x.
(3)由題意2x+1500=4000,x=1250,
5x=4000,x=800,
1250>800,
∴甲印刷廠印制的宣傳材料份數較多.
點評 本題考查的是一次函數的應用問題,解題關鍵是要讀懂題目的意思,根據題目給出的條件,找出合適的等量關系,列出函數式,再求解.


 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:初中數學 來源: 題型:解答題
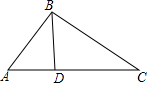 如圖,在△ABC中,D是AC上一點,聯結BD,∠CBD=∠A.
如圖,在△ABC中,D是AC上一點,聯結BD,∠CBD=∠A.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
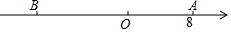 如圖,已知數軸上點A表示的數為8,B是數軸上位于點A左側一點,且AB=20,動點P從A點出發,以每秒5個單位長度的速度沿數軸向左勻速運動,設運動時間為t(t<0)秒.
如圖,已知數軸上點A表示的數為8,B是數軸上位于點A左側一點,且AB=20,動點P從A點出發,以每秒5個單位長度的速度沿數軸向左勻速運動,設運動時間為t(t<0)秒.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 閱讀下面的材料,回答問題:
閱讀下面的材料,回答問題:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com