
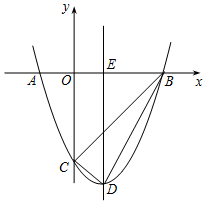
 如圖,拋物線y=x2+bx+c與x軸交于A(-1,0)和B(3,0)兩點,與y軸交于點C,對稱軸與x軸交于點E,點D為頂點,連接BD、CD、BC.
如圖,拋物線y=x2+bx+c與x軸交于A(-1,0)和B(3,0)兩點,與y軸交于點C,對稱軸與x軸交于點E,點D為頂點,連接BD、CD、BC.分析 (1)先利用待定系數法求二次函數的解析式,并配方成頂點式求頂點D的坐標,和與y軸的交點C的坐標,由勾股定理計算△BDC三邊的平方,利用勾股定理的逆定理證明△BCD是直角三角形;
(2)作輔助線,構建直角三角形PCQ與直角三角形BDC相似,根據比例式表示出點P的坐標,利用待定系數法求直線BD的解析式,因為點P為線段BD上一點,代入直線BD的解析式列方程可求出點P的坐標;
(3)同理求直線CD的解析式為:y=-x-3,由此表示點N的坐標為(a,-a-3),因為M在拋物線上,所以設M(x,x2-2x-3),根據同角的三角函數得:tan∠BDE=tan∠CMN=$\frac{1}{2}$,則$\frac{CN}{MN}=\frac{1}{2}$,
如圖2,證明△MGN∽△NFC,列比例式可得方程組解出即可;
如圖3,證明△CFN∽△NGM,列比例式可得方程組解出即可.
解答 解:(1)把A(-1,0)和B(3,0)兩點代入拋物線y=x2+bx+c中得:
$\left\{\begin{array}{l}{1-b+c=0}\\{9+3b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
∴拋物線的解析式為:y=x2-2x-3=(x-1)2-4,
∴C(0,-3),D(1,-4),
由勾股定理得:BC2=32+32=18,
CD2=12+(4-3)2=2,
BD2=(3-1)2+42=20,
∴CD2+BC2=BD2,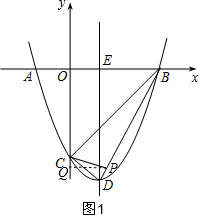
即∠BCD=90°,
∴△BCD是直角三角形;
(2)作PQ⊥OC于點Q,
∴∠PQC=90°,
∵∠PCO+∠CDB=180°,
∠PCO+∠PCQ=180°,
∴∠CDB=∠PCQ,
∵∠PQC=∠BCD=90°,
∴△PCQ∽△BDC,
∴$\frac{PQ}{CQ}=\frac{BC}{DC}=\frac{3\sqrt{2}}{\sqrt{2}}$=3,
∴PQ=3CQ,
設CQ=m,則PQ=3m,
設P(3m,-3-m),
設直線BD的解析式為:y=kx+b,
把B(3,0)、D(1,-4)代入得:$\left\{\begin{array}{l}{3k+b=0}\\{k+b=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-6}\end{array}\right.$,
∴直線BD的解析式為:y=2x-6,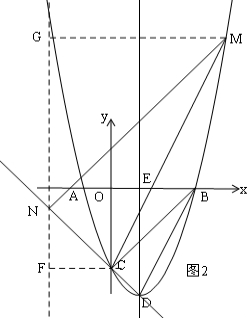
將點P的坐標代入直線BD:y=2x-6得:
-3-m=2×3m-6,
m=$\frac{3}{7}$,
∴3m=$\frac{9}{7}$,-3-m=-3-$\frac{3}{7}$=-$\frac{24}{7}$,
∴P($\frac{9}{7}$,-$\frac{24}{7}$);
(3)∵∠CMN=∠BDE,
∴tan∠BDE=tan∠CMN=$\frac{BE}{DE}=\frac{3-1}{4}$=$\frac{1}{2}$,
∴$\frac{CN}{MN}=\frac{1}{2}$,
同理可求得:CD的解析式為:y=-x-3,
設N(a,-a-3),M(x,x2-2x-3),
①如圖2,過N作GF∥y軸,過M作MG⊥GF于G,過C作CF⊥GF于F,
則△MGN∽△NFC,
∴$\frac{MG}{FN}=\frac{NG}{FC}$=$\frac{MN}{NC}=\frac{2}{1}$,
∴$\frac{x-a}{3-a-3}=\frac{{x}^{2}-2x-3+a+3}{-a}$=2,
則$\left\{\begin{array}{l}{x-a=-2a}\\{{x}^{2}-2x-3+a+3=-2a}\end{array}\right.$,
∴x1=0(舍),x2=5,
當x=5時,x2-2x-3=12,
∴M(5,12),
②如圖3,過N作FG∥x軸,交y軸于F,過M作MG⊥GF于G,
∴△CFN∽△NGM,
∴$\frac{FC}{NG}=\frac{FN}{MG}$=$\frac{1}{2}$,
∴$\frac{a+3-3}{x-a}$=$\frac{a}{a+3-(-{x}^{2}+2x+3)}$=$\frac{1}{2}$,
則$\left\{\begin{array}{l}{x-a=2a}\\{2a=a+3+{x}^{2}-2x-3}\end{array}\right.$,
∴x1=0(舍),x2=$\frac{7}{3}$,
當x=$\frac{7}{3}$時,y=x2-2x-3=-$\frac{20}{9}$,
∴M($\frac{7}{3}$,-$\frac{20}{9}$),
綜上所述,點M的坐標(5,12)或($\frac{7}{3}$,-$\frac{20}{9}$).
點評 本題是二次函數的綜合題,考查了利用待定系數法求二次函數和一次函數的解析式,還考查了勾股定理的逆定理、相似三角形的性質和判定,并掌握利用解析式表示點的坐標,根據已知條件列方程或方程組求出未知數的值,本題的第二問和第三問都是證明三角形相似解決問題.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:初中數學 來源: 題型:選擇題
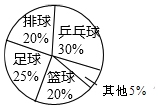 如圖是某班學生最喜歡的球類活動人數統計圖,則下列說法不正確的是( )
如圖是某班學生最喜歡的球類活動人數統計圖,則下列說法不正確的是( )| A. | 該班喜歡乒乓球的學生最多 | |
| B. | 該班喜歡排球和籃球的學生一樣多 | |
| C. | 該班喜歡足球的人數是喜歡排球人數的1.25倍 | |
| D. | 該班喜歡其他球類活動的人數為5人 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
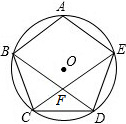 如圖,五邊形ABCDE內接于⊙O,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$=$\widehat{AE}$,BD和CE相交于點F,不添加輔助線,則圖中有5個等腰三角形.
如圖,五邊形ABCDE內接于⊙O,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$=$\widehat{AE}$,BD和CE相交于點F,不添加輔助線,則圖中有5個等腰三角形.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 若a>0,b<0,則$\frac{b}{a}$>0 | B. | 若a>b,則a-b>0 | ||
| C. | 若a<0,b<0,則ab<0 | D. | 若a>b,a<0,則$\frac{b}{a}$<0 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0個 | B. | 1個 | C. | 2個 | D. | 3個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com