Question

11．將△ABC繞點A按逆時針方向旋轉θ度，并使各邊長變?yōu)樵瓉淼膎倍，得△AB′C′，如圖①，我們將這種變換記為[θ，n]．
（1）如圖①，對△ABC作變換[50°，$\sqrt{5}$]得△AB′C′，則S_△AB′C′：S_△ABC=5：1；直線BC與直線B'C′所夾的銳角為50度；
（2）如圖②，△ABC中，∠BAC=30°，∠ACB=90°，對△ABC 作變換[θ，n]得△AB'C'，使點B、C、C′在同一直線上，且四邊形ABB'C'為矩形，求θ 和n的值；
（3）如圖③，△ABC中，AB=AC，∠BAC=36°，BC=l，對△ABC作變換[θ，n]得△AB′C′，使點B、C、B′在同一直線上，且四邊形ABB'C'為平行四邊形，求θ 和n的值．

Answer 1

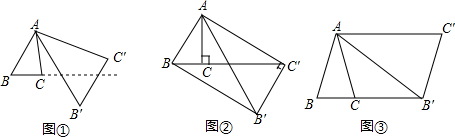
分析 （1）如圖①，根據(jù)題意可知：△ABC∽△AB'C'，由相似三角形面積比等于相似比的平方得出結論；在△ABN和△B′MN中，兩個角對應相等，則第三個角相等，即∠BMB'=∠BAB'=50°；
（2）如圖②，根據(jù)∠BAC=30°，∠ACB=90°可以求旋轉角∠CAC′的度數(shù)，在Rt△ABB′中，利用30°角所對的直角邊是斜邊的一半可以求得n的值；
（3）如圖③，先根據(jù)等腰三角形的兩個底角相等，得∠ACB=72°，由平行四邊形性質(zhì)得：AC′∥BB′，所以
θ=∠CAC'=72°，證明△ABC∽△B'BA，列比例式可求AB的長，即B′C′的長，計算n=$\frac{B′C′}{BC}$=$\frac{AB}{BC}$=$\frac{1+\sqrt{5}}{2}$．

解答 解：（1）如圖①，根據(jù)題意得：△ABC∽△AB'C'，
∴S_△AB'C'：S_△ABC=（$\frac{AB′}{AB}$）²=（$\frac{\sqrt{5}}{1}$）²=5：1，∠B=∠B'，
∵∠ANB=∠B'NM，
∴∠BMB'=∠BAB'=50°；
故答案為：5：1，50；
（2）如圖②，∵四邊形 ABB'C'是矩形，
∴∠BAC'=90°，
∴θ=∠CAC'=∠BAC'-∠BAC=90°-30°=60°，
在Rt△ABB′中，∠ABB'=90°，∠BAB'=60°，
∴∠AB'B=30°，
∴AB′=2AB，
∴n=$\frac{AB′}{AB}$=2；
（3）如圖③，∵AB=AC，∠BAC=36°，
∴∠B=∠ACB=72°，
∵四邊形ABB'C'是平行四邊形，
∴AC'∥BB'，
∴∠CAC'=∠ACB=72°，
∴θ=∠CAC'=72°，
∴∠BAB'=∠CAC'=72°，
∴∠BB'A=36°，
∴∠BB'A═∠BAC=36°，而∠B=∠B，
∴△ABC∽△B'BA，
∴AB：BB'=CB：AB，
∴AB²=CB•BB'=CB（BC+CB'），
∵∠ACB=72°，∠AB′B=36°，
∴∠CAB′=36°，
∴∠CAB′=∠AB′B，
∴CA=CB′，
∴CB'=CA=AB=B'C'，
∵BC=1，
∴AB²=1×（1+AB），
∴AB=$\frac{1±\sqrt{5}}{2}$，
∵AB＞0，
∴$AB=\frac{1+\sqrt{5}}{2}$，
∴n=$\frac{B′C′}{BC}$=$\frac{AB}{BC}$=$\frac{1+\sqrt{5}}{2}$．

點評 本題是四邊形的綜合題，考查了矩形、平行四邊形、旋轉的幾何變換問題，和以往的旋轉不同，既旋轉一定的角度，邊長又擴大一定的倍數(shù)，所以要認真理解題意，本題還屬于新定義的問題，此類題考查了學生的能力，也有助于學生的能力的培養(yǎng)．