Question

2．已知平行四邊形ABCD，AC與BD交于O點(diǎn)，EF過點(diǎn)O且EF⊥AB，AC=$\sqrt{5}$EF，∠ACB=45°．
（1）圖中有6對全等三角形；
（2）求證：OA平分∠DOE；
（3）求S_{四邊形ADOE}：S_{四邊形ABCD}．

Answer 1

分析 （1）根據(jù)平行四邊形的性質(zhì)可得出OA=OC，OB=OD，根據(jù)全等三角形的判定方法可得出6對全等三角形；
（2）根據(jù)EF⊥AB，可得出OA=$\sqrt{5}$OE，根據(jù)勾股定理即可得出AE=2OE=EF，作AH⊥CD，交CD的延長線于H，得四邊形AEFH為正方形，求得AE=AH，△ADH順時(shí)針旋轉(zhuǎn)90°，使H與E重合，得到△AGE，從而得到∠HAD=∠EAG，AG=AD，進(jìn)一步求得∠GAO=∠DAO=45°，然后根據(jù)SAS證得△AOD≌△AOG，即可證得結(jié)論；
（3）由（2）可知OD=OE+DH，設(shè)OE=OF=a，DH=a，則OD=a+x，DF=2a-x，在RT△ODF中利用勾股定理求出a與x的關(guān)系可以解決問題．

解答 解：（1）∵四邊形ABCD是平行四邊形，
∴OA=OC，OB=OD，AD=BC，AB=CD，AB∥CD，
∴∠OAE=∠OCF，
在△AOE和△COF中，
$\left\{\begin{array}{l}{∠OAE=∠OCF}\\{∠AOE=∠COF}\\{OA=OC}\end{array}\right.$，
∴△AOE≌△COF（AAS），
同理可得：△BOE≌△DOF，
在△AOD和△COB中，
$\left\{\begin{array}{l}{OA=OC}\\{AD=CB}\\{OD=OB}\end{array}\right.$，
∴△AOD≌△COB（SSS），
同理可得：△AOB≌△COD，△ACD≌△CAB，△ABD≌△CDB．
故答案為：6；

（2）如圖1，∵AC=$\sqrt{5}$EF，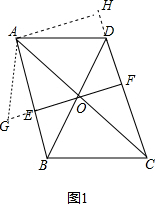
∴OA=$\sqrt{5}$OE，
∵AE²=OA²-OE²，
∴AE²=4OE²，
∴AE=2OE，
∴AE=EF，
作AH⊥CD，交CD的延長線于H，得四邊形AEFH為正方形，
∴AE=AH，
延長FE到G，使EG=DH，連接AG，
∴△ADH≌△AGE（SAS），
∴∠HAD=∠EAG，AG=AD，
∵∠ACB=∠DAC=45°，
∵AH⊥AE，
∴∠HAD+∠EAO=45°，
∴∠GAO=∠DAO=45°，
在△AOD和△AOG中
$\left\{\begin{array}{l}{AG=AD}\\{∠GAO=∠DAO}\\{OA=OA}\end{array}\right.$
∴△AOD≌△AOG（SAS），
∴∠AOD=∠AOE，
∴OA平分∠DOE；

（3）設(shè)OE=OF=a，DH=x，由（2）可知DO=OG=OE+EG=OE+DH=a+x，AE=HF=2a，DF=2a-x，
在RT△DOF中，∵DO²=OF²+DF²，
∴（a+x）²=a²+（2a-x）²，
∴X=$\frac{2}{3}a$，易知：DF=EB=2a-$\frac{2}{3}$a=$\frac{4}{3}$a，
∴AE：EB=3：2，
∵ABCD是平行四邊形，
∴可以設(shè)S_△AOD=S_△AOB=5K，則易知：S_{平行四邊形ABCD}=20K，S_△AOE=3K，
∴S_{四邊形ADOE}=8K，
∴S_{四邊形ADOE}：S_{平行四邊形ABCD}=8K：20K=2：5．

點(diǎn)評 此題考查了平行四邊形，正方形的性質(zhì)以及利用勾股定理解決邊之間的關(guān)系．注意45°角在本題目中的作用．