
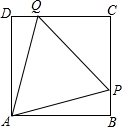
 如圖,在邊長為10的正方形ABCD中,△PAQ是正三角形,求PB的長.
如圖,在邊長為10的正方形ABCD中,△PAQ是正三角形,求PB的長. 分析 設PB=x,根據正方形以及等邊三角形的性質求出PQ與PC的表達式,然后利用勾股定理列出方程求出x的值.
解答 解:設PB=x,
∴PC=10-x,
由題意可知:AD=AB,AQ=AP
在Rt△AQD與Rt△APB中,
$\left\{\begin{array}{l}{AQ=AP}\\{AD=AB}\end{array}\right.$
∴Rt△AQD≌Rt△APB(HL)
∴DQ=PB=x,
∴CQ=10-x,
在Rt△APB中,AP2=100+x2,
在Rt△CQP中,AP2=CQ2+PC2,
∴100+x2=2(10-x)2
化簡:x2-40x+100=0,
解得:x=20±10$\sqrt{3}$,
∵x<10,
∴PB=x=20-10$\sqrt{3}$
點評 本題考查正方形以及等邊三角形的性質,涉及勾股定理,全等三角形的判定與性質,一元二次方程的解法.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
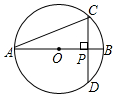 如圖,AB是⊙O的直徑,弦CD⊥AB,垂足為點P,若AB=4,AC=2$\sqrt{3}$,
如圖,AB是⊙O的直徑,弦CD⊥AB,垂足為點P,若AB=4,AC=2$\sqrt{3}$,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在2016年寶應以“不忘初心,繼續前進”為主題的青年千人毅行中,隨機抽得12名選手所用的時間(單位:分鐘)得到如下樣本數據:
在2016年寶應以“不忘初心,繼續前進”為主題的青年千人毅行中,隨機抽得12名選手所用的時間(單位:分鐘)得到如下樣本數據:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
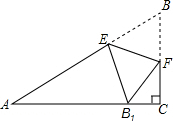 如圖,在△ABC中,∠C=90°,點E,F分別在邊AB,BC上,沿直線EF將△EBF翻折,使頂點B的對應點B1落在AC邊上,且EB1⊥AC.求證:四邊形BFB1E是菱形.
如圖,在△ABC中,∠C=90°,點E,F分別在邊AB,BC上,沿直線EF將△EBF翻折,使頂點B的對應點B1落在AC邊上,且EB1⊥AC.求證:四邊形BFB1E是菱形.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com