
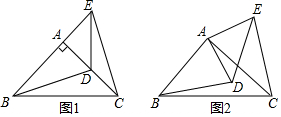
分析 (1)延長BD與EC交于點F,可以證明△ACE≌△ADB,可得BD=CE,且∠BFE=90°,即可解題;
(2)BD=CE,BD⊥CE.根據全等三角形的判定定理SAS推知△ABD≌△ACE,然后由全等三角形的對應邊相等證得BD=CE、對應角相等∠ABF=∠ECA;延長BD交AC于F,交CE于H,構建對頂角∠ABF=∠HCF,再根據三角形內角和定理證得∠BHC=90°.
解答 解:(1)延長BD與EC交于點F,
在△ACE和△ADB中,
∵$\left\{\begin{array}{l}{AE=AD}\\{∠EAC=∠DAB}\\{AC=AB}\end{array}\right.$,
∴△ACE≌△ADB(SAS),
∴BD=CE,∠AEC=∠ADB,
∵∠ADB+∠ABD=90°
∴∠ABD+∠AEC=90°
∴∠BFE=90°,
∴BD⊥CE.
故答案為:相等,垂直;
(2)成立,
∵∠BAC=∠DAE=90°
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,
在△ABD與△ACE中,
∵$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$
∴△ABD≌△ACE(SAS)
∴BD=CE,
延長BD交AC于F,交CE于H.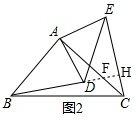
在△ABF與△HCF中,
∵∠ABF=∠HCF,∠AFB=∠HFC
∴∠CHF=∠BAF=90°,
∴BD⊥CE.
點評 本題主要考查等腰直角三角形的性質、全等三角形的判定與性質及三角形的內角和定理,根據等腰三角形的性質得出三角形的兩條邊相等,據此根據判定證三角形的全等是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
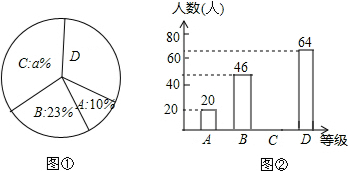 一家公司對一種新研發的手機進行市場問卷調查,其中一個項目是讓每個人按A(不喜歡)、B(一般)、C(比較喜歡)、D(非常喜歡)四個等級對該手機進行評價,圖①和圖②是該公司采集數據后,繪制的兩幅不完整的統計圖,請你根據以上統計圖提供的信息,回答下列問題:
一家公司對一種新研發的手機進行市場問卷調查,其中一個項目是讓每個人按A(不喜歡)、B(一般)、C(比較喜歡)、D(非常喜歡)四個等級對該手機進行評價,圖①和圖②是該公司采集數據后,繪制的兩幅不完整的統計圖,請你根據以上統計圖提供的信息,回答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
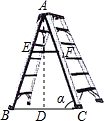 如圖,已知“人字梯”的5個踩檔把梯子等分成6份,從上往下的第二個踩檔與第三個踩檔的正中間處有一條60cm長的綁繩EF,tanα=$\frac{5}{2}$,則“人字梯”的頂端離地面的高度AD是180cm.
如圖,已知“人字梯”的5個踩檔把梯子等分成6份,從上往下的第二個踩檔與第三個踩檔的正中間處有一條60cm長的綁繩EF,tanα=$\frac{5}{2}$,則“人字梯”的頂端離地面的高度AD是180cm.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,O是正△ABC內一點,OA=3,OB=4,OC=5,將線段BO以點B為旋轉中心逆時針旋轉60°得到線段BO′,下列結論:①△BO′A可以由△BOC繞點B逆時針旋轉60°得到;②點O與O′的距離為4;③∠AOB=150°;④S四邊形AOBO′=6+3$\sqrt{3}$.其中正確的結論是①②③.
如圖,O是正△ABC內一點,OA=3,OB=4,OC=5,將線段BO以點B為旋轉中心逆時針旋轉60°得到線段BO′,下列結論:①△BO′A可以由△BOC繞點B逆時針旋轉60°得到;②點O與O′的距離為4;③∠AOB=150°;④S四邊形AOBO′=6+3$\sqrt{3}$.其中正確的結論是①②③.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
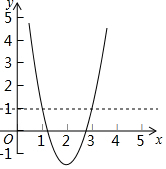 如圖,二次函數y=ax2+bx+c(a>0)的圖象與直線y=1交點坐標為(1,1),(3,1),則不等式ax2+bx+c-1>0的解集為( )
如圖,二次函數y=ax2+bx+c(a>0)的圖象與直線y=1交點坐標為(1,1),(3,1),則不等式ax2+bx+c-1>0的解集為( )| A. | x>1 | B. | 1<x<3 | C. | x<1或x>3 | D. | x>3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com