Question

4．如圖△ABC中，∠B=60°，∠C=78°，點D在AB邊上，點E在AC邊上，且DE∥BC，將△ADE沿DE折疊，點A對應點為F點．
（1）若點A落在BC邊上（如圖1），求證：△BDF是等邊三角形；
（2）若點A落在三角形外（如圖2），且CF∥AB，求△CEF各內角的度數．

Answer 1

分析 （1）利用平行線的性質得出∠ADE=60°，再利用翻折變換的性質得出∠ADE=∠EDF=60°，進而得出∠BDF=60°即可得出答案；
（2）利用平行線的性質結合（1）中所求得出∠2，∠5+∠6的度數即可得出答案．

解答 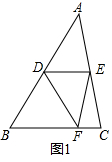（1）證明：如圖1，∵∠B=60°，DE∥BC，
∴∠ADE=60°，
∵△ADE沿DE折疊，點A對應點為F點，
∴∠ADE=∠EDF=60°，
∴∠BDF=60°，
∴△BDF是等邊三角形；

（2）解：如圖2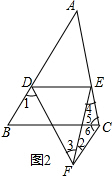，由（1）得：∠1=60°，
∵CF∥AB，
∴∠2+∠3=60°，∠B=∠6=60°，
∵∠B=60°，∠C=78°，
∴∠A=∠3=42°，
∴∠2=60°-42°=18°，
∴∠5+∠6=60°+78°=138°，
∴∠4=∠180°-18°-138°=24°．

點評 此題主要考查了翻折變換的性質以及平行線的性質和等邊三角形的判定以及三角形內角和定理等知識，正確利用翻折變換的性質得出∠ADE=∠EDF是解題關鍵．