
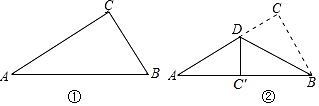
| A. | $\frac{10}{3}$cm | B. | $\frac{8}{3}$cm | C. | $\frac{5}{2}$cm | D. | $\sqrt{5}$cm |
分析 利用勾股定理列式求出AC,根據翻折變換的性質可得BC′=BC,DC′=DC,設DC=x,表示出AD,然后利用勾股定理列方程求解即可.
解答 解:∵∠C=Rt∠,AB=13cm,BC=5cm,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12cm,
∵折疊點C落在斜邊上的點C′處,
∴BC′=BC=5,DC′=DC,
∴AC′=AB-BC′=13-5=8cm,
設DC=x,則AD=AC-DC=12-x,
DC′=x,
在Rt△AC′D中,根據勾股定理得,AC′2+DC′2=AD2,
即82+x2=(12-x)2,
解得x=$\frac{10}{3}$,
所以,DC的長為$\frac{10}{3}$cm.
故選A.
點評 本題考查了翻折變換,勾股定理,翻折前后對應線段相等,對應角相等,此類題目,利用勾股定理列出方程是解題的關鍵.


科目:初中數學 來源: 題型:填空題
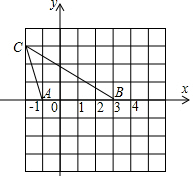 △ABC在平面直角坐標系中的位置如圖所示,現另有一點D,滿足以A,B,D為頂點的三角形與△ABC全等,則D點坐標為(4,3)或(-2,-3)或(4,-3).
△ABC在平面直角坐標系中的位置如圖所示,現另有一點D,滿足以A,B,D為頂點的三角形與△ABC全等,則D點坐標為(4,3)或(-2,-3)或(4,-3).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com