Question

19．如圖，拋物線y=ax²+bx-4a經過A（-1，0），C（0.4）兩點，與x軸交于另一點B．
（1）求拋物線的解析式；
（2）點P為拋物線第一象限上的點，求四邊形PBOC的最大面積；
（3）已知點D（m，m+1）在第一象限的拋物線上，求點D關于直線BC對稱的點的坐標．

Answer 1

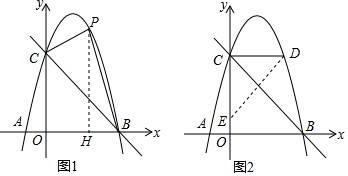
分析 （1）直接將點A（-1，0），C（0.4）兩點代入拋物線解析式y=ax²+bx-4a，解得a，b，可得結果；
（2）由（1）的結果，可設點P的坐標是（x，-x²+3x+4）解得點B的坐標，利用梯形和三角形的面積公式可得四邊形PBOC的面積，利用二次函數的最值可得最大面積；
（3）由點D（m，m+1）在第一象限的拋物線上可得m的值，易得點D的坐標，可得∠OBC=45°，易得CD∥AB且CD=3，設點D關于直線BC的對稱點為點E，可得點E在y軸上，且CE=CD=3，易得點E的坐標，即得結果．

解答 解：（1）∵拋物線y=ax²+bx-4a經過C（0.4），
∴-4a=4，
a=-1，
將A（-1，0）代入y=-x²+bx+4，得
-1-b+4=0，
∴b=3．
∴拋物線的解析式為y=-x²+3x+4；    

（2）由已知，可設點P的坐標是（x，-x²+3x+4）
如圖1，作PH⊥x軸于H，則OH=x，PH=-x²+3x+4，
由（1），當-x²+3x+4=0時，解得x=-1或x=4，
∴點B的坐標是（4，0），∴OB=4；
∵點C的坐標是（0，4），∴OC=4．
∴S_{四邊形PBOC}=S_{四邊形PHOC}+S_△PHB=$\frac{1}{2}$（OC+PH）•OH$+\frac{1}{2}$PH•BH
=$\frac{1}{2}OC•OH$$+\frac{1}{2}$PH（OC+BH）=$\frac{1}{2}OC•OH$$+\frac{1}{2}PH•OB$
=$\frac{1}{2}×4x+\frac{1}{2}$（-x²+3x+4）×4
=-2x²+8x+8
=-2（x-2）²+16
∴當x=2時，四邊形PBOC的最大面積是16；

（3）∵點D（m，m+1）在第一象限的拋物線上，
∴m+1=-m²+3m+4，
∴m²-2m-3=0，
∴m=-1或m=3．
∵點D在第一象限，
∴點D的坐標為（3，4），
如圖2，由（1）知，OB=OC=4，
∴∠OBC=45°，
設點D關于直線BC的對稱點為點E，
∵C（0，4），∴CD∥AB且CD=3，
∴∠ECB=∠DCB=45°，
∴點E在y軸上，且CE=CD=3，
∴OE=1，
∴點E的坐標為（0，1）．
即點D關于直線BC對稱的點的坐標為（0，1）．

點評 本題主要考查了二次函數的最值及拋物線與x軸的交點，能夠根據二次函數的解析式得出各點坐標是解答此題的關鍵．