Question

3．如圖所示，點A是半圓上一個三等分點，點B是$\widehat{AN}$的中點，點P是直徑 MN上一動點，若⊙O的直徑為2，則AP+BP的最小值是$\sqrt{2}$．

Answer 1

分析 作點B關(guān)于MN的對稱點B′，連接AB′交MN于點P，連接BP，由三角形兩邊之和大于第三邊即可得出此時AP+BP=AB′最小，連接OB′，根據(jù)點A是半圓上一個三等分點、點B是$\widehat{AN}$的中點，即可得出∠AOB′=90°，再利用勾股定理即可求出AB′的值，此題得解．

解答 解：作點B關(guān)于MN的對稱點B′，連接AB′交MN于點P，連接BP，此時AP+BP=AB′最小，連接OB′，如圖所示．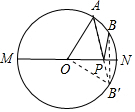
∵點B和點B′關(guān)于MN對稱，
∴PB=PB′．
∵點A是半圓上一個三等分點，點B是$\widehat{AN}$的中點，
∴∠AON=180°÷3=60°，∠B′ON=∠AON÷2=30°，
∴∠AOB′=∠AON+∠B′ON=90°．
∵OA=OB′=1，
∴AB′=$\sqrt{2}$．
故答案為：$\sqrt{2}$．

點評 本題考查了圓心角、弧、弦的關(guān)系、軸對稱中最短路線問題、三角形的三邊關(guān)系以及勾股定理，根據(jù)三角形的三邊關(guān)系確定AP+BP取最小值時點P的位置是解題的關(guān)鍵．