
 解方程:
解方程:分析 (1)確定a,b,c的值,求出b2-4ac的值,在b2-4ac≥0的前提下,把a、b、c的值代入公式進行計算求出方程的根;
(2)方程兩邊同除以二次項系數,使二次項系數為1,并把常數項移到方程右邊;方程兩邊同時加上一次項系數一半的平方;把左邊配成一個完全平方式,右邊化為一個常數;如果右邊是非負數,就可以進一步通過直接開平方法來求出它的解;
(3)把一條線段分成兩部分,使其中較長的線段為全線段與較短線段的比例中項,這樣的線段分割叫做黃金分割,據此求得黃金比.
解答 解:(1)2x2-5x+1=0
∵a=2,b=-5,c=1,
∴△=25-8=17>0,
∴${x}_{1}=\frac{5+\sqrt{17}}{4}$,${x}_{2}=\frac{5-\sqrt{17}}{4}$;
(2)2x2-4x-1=0
2(x2-2x+1-1)=1,
2(x-1)2-2=1,
2(x-1)2=3,
(x-1)2=$\frac{3}{2}$,
∴x-1=±$\frac{\sqrt{6}}{2}$,
∴${x}_{1}=1+\frac{\sqrt{6}}{2}$,${x}_{2}=1-\frac{\sqrt{6}}{2}$;
(3)設線段AB=1,較長的線段AC的長為x,
∵C是線段AB的黃金分割點,
∴AC2=AB•BC,
x2=1•(1-x),
解得:${x}_{1}=\frac{-1+\sqrt{5}}{2}$,${x}_{2}=\frac{-1-\sqrt{5}}{2}$(舍去負值),
∴$\frac{AC}{AB}$=$\frac{x}{1}$=$\frac{\sqrt{5}-1}{2}$,
答:黃金比為$\frac{\sqrt{5}-1}{2}$.
點評 本題主要考查了運用公式法和配方法解一元二次方程,以及黃金分割,解題時注意:把線段AB分成兩條線段AC和BC(AC>BC),且使AC是AB和BC的比例中項,叫做把線段AB黃金分割,點C叫做線段AB的黃金分割點.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:填空題
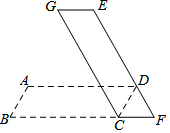 如圖,將平行四邊形ABCD繞點C順時針旋轉一定角度α(0°<α<180°)后,得到平行四邊形EFCG,若BC與CF在同一直線上,且點D恰好在EF上,則α=60°.
如圖,將平行四邊形ABCD繞點C順時針旋轉一定角度α(0°<α<180°)后,得到平行四邊形EFCG,若BC與CF在同一直線上,且點D恰好在EF上,則α=60°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
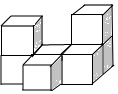 (1)用7個相同的小正方體拼了一個幾何體,畫出幾何體從左面和和上面看到的形狀圖;
(1)用7個相同的小正方體拼了一個幾何體,畫出幾何體從左面和和上面看到的形狀圖;查看答案和解析>>
科目:初中數學 來源: 題型:解答題
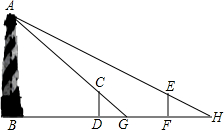 如圖,某水平地面上建筑物的高度為AB,在點D和點F處分別豎立高是2米的標桿CD和EF,兩標桿相隔52米,并且建筑物AB、標桿CD和EF在同一豎直平面內,從標桿CD后退2米到點G處,測得G處、標桿頂端C和建筑物頂端A在同一條直線上;從標桿FE后退4米到點H處,測得H處、標桿頂端E和建筑物頂端A在同一條直線上,AB⊥BH,CD⊥BH,EF⊥BH,求建筑物AB的高.
如圖,某水平地面上建筑物的高度為AB,在點D和點F處分別豎立高是2米的標桿CD和EF,兩標桿相隔52米,并且建筑物AB、標桿CD和EF在同一豎直平面內,從標桿CD后退2米到點G處,測得G處、標桿頂端C和建筑物頂端A在同一條直線上;從標桿FE后退4米到點H處,測得H處、標桿頂端E和建筑物頂端A在同一條直線上,AB⊥BH,CD⊥BH,EF⊥BH,求建筑物AB的高.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
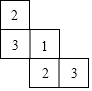 一個幾何體由大小相同的小立方體搭成,從上面看到的幾何體的形狀圖如圖所示,其中小正方形中的數字表示在該位置的小立方塊的個數,請畫出從正面和左面看到的這個幾何體的形狀圖.
一個幾何體由大小相同的小立方體搭成,從上面看到的幾何體的形狀圖如圖所示,其中小正方形中的數字表示在該位置的小立方塊的個數,請畫出從正面和左面看到的這個幾何體的形狀圖.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com