
 如圖,一次函數y=-x+4的圖象與x軸、y軸分別相交于點A、B,過點A作x軸的垂線l,點P為直線l上的動點,點Q為直線AB與△OAP外接圓的交點,點P、Q與點A都不重合.
如圖,一次函數y=-x+4的圖象與x軸、y軸分別相交于點A、B,過點A作x軸的垂線l,點P為直線l上的動點,點Q為直線AB與△OAP外接圓的交點,點P、Q與點A都不重合.分析 (1)將y=0代入y=-x+4,求得x的值,從而得到點A的坐標;
(2)首先根據題意畫出圖形,然后在Rt△BOA中,由勾股定理得:AB的長度,然后由全等三角形的性質求得QA的長度,從而得到BQ的長,然后根據PA=BQ求得PA的長度,從而可求得點P的坐標;
(3)首先根據題意畫出圖形,設AP=m,由△OAM∽△PAO,可求得AM的長度,然后根據勾股定理可求得兩圓的直徑(用含m的式子表示),然后利用圓的面積公式求得兩圓的面積,最后代入所求代數式求解即可.
解答 解(1)令y=0,得:-x+4=0,解得x=4,
即點A的坐標為(4,0);
(2)存在.
理由:第一種情況,如下圖一所示: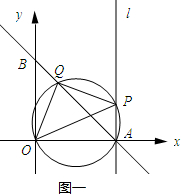
∵∠OBA=∠BAP,∴它們是對應角,
∴BQ=PA,
將x=0代入y=-x+4得:y=4,
∴OB=4,
由(1)可知OA=4,
在Rt△BOA中,由勾股定理得:AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=4$\sqrt{2}$.
∵△BOQ≌△AQP.
∴QA=OB=4,BQ=PA.
∵BQ=AB-AQ=4$\sqrt{2}$-4,
∴PA=4$\sqrt{2}$-4.
∴點P的坐標為(4,4$\sqrt{2}$-4);
第二種情況,如下圖二所示: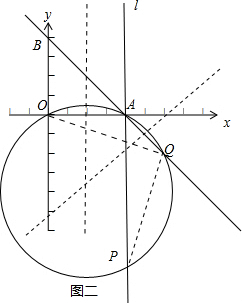
∵△OQB≌△APQ,
∴AQ=BO=4,AB=$\sqrt{{4}^{2}+{4}^{2}}=4\sqrt{2}$,BQ=AP,
∴BQ=AB+AQ=$4\sqrt{2}+4$,
∴AP=4$\sqrt{2}+4$,
∴點P的坐標為:(4,-4$\sqrt{2}-4$);
由上可得,點P的坐標為:(4,$4\sqrt{2}-4$)或(4,$-4\sqrt{2}-4$).
(3)如圖所示: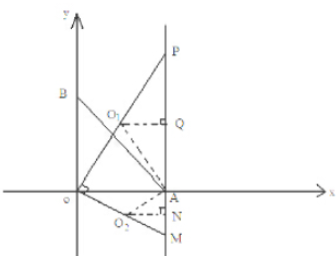
令PA=a,MA=b,△OAP外接圓的圓心為O1,△OAM的外接圓的圓心為O2,
∴OP2=OA2+PA2=42+a2=16+a2,OM2=OA2+MA2=42+b2=16+b2,
在Rt△POM中,PM2=OP2+OM2=a2+16+b2+16,
又∵PM2=(PA+AM)2=(a+b)2=a2+2ab+b2,
∴ab=16,
∵O1A2=O1Q2+QA2=($\frac{OA}{2}$)2+($\frac{PA}{2}$)2=$\frac{1}{4}$a2+4,O2A2=O2N2+NA2=($\frac{OA}{2}$)2+($\frac{MA}{2}$)2=$\frac{1}{4}$b2+4,
∴S1=π×O1A2=($\frac{1}{4}$a2+4)π,S2=π×O2A2=($\frac{1}{4}$b2+4)π,
∴$\frac{1}{{S}_{1}}+\frac{1}{{S}_{2}}$=$\frac{{S}_{1}+{S}_{2}}{{S}_{1}{S}_{2}}$=$\frac{π×(\frac{1}{4}{a}^{2}+4)+π×(\frac{1}{4}{b}^{2}+4)}{π×(\frac{1}{4}{a}^{2}+4)×π×(\frac{1}{4}{b}^{2}+4)}$=$\frac{4}{π}$×$\frac{{a}^{2}+{16+b}^{2}+16}{16{a}^{2}+16{b}^{2}+1{6}^{2}+1{6}^{2}}$=$\frac{1}{4π}$.
點評 本題主要考查的是全等三角形的性質,相似三角形的性質和判定以及勾股定理和一次函數的綜合應用,根據題意畫出圖形,利用全等三角形和相似三角形的性質和判定求得AM和PA的長度是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
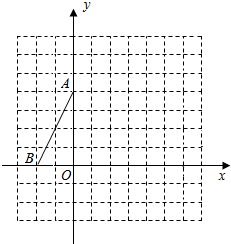 如圖,在平面直角坐標系中,O是坐標原點,點A、B的坐標分別為A(0,4)和B(-2,0),連結AB.
如圖,在平面直角坐標系中,O是坐標原點,點A、B的坐標分別為A(0,4)和B(-2,0),連結AB.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com