Question

9．如圖，時鐘的時針，分針均按時正常轉動．
（1）分針每分針轉動了6度，時針每分鐘轉動了0.5度；
（2）若現在時間恰好是2點整，求：
①經過多少分鐘后，時針與分針第一次成90°角；
②從2點到4點（不含2點）有幾次時針與分針成60°角，分別是幾時幾分？

Answer 1

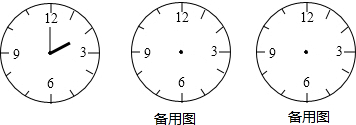
分析 （1）利用鐘表表盤的特征解答．表盤共被分成60小格，每一小格所對角的度數為6°．
（2）①可設經過x分鐘后，時針與分針第一次成90°角，根據角度差的等量關系列出方程求解即可；
②分三種情況：2時～3時，時針與分針成60°角；3時～4時，時針在前面，分針在后面，時針與分針成60°角；3時～4時，分針在前面，時針在后面，時針與分針成60°角；列出方程求解即可．

解答 解：（1）分針每分針轉動了6度，時針每分鐘轉動了0.5度．
故答案為：6，0.5；
（2）①設經過x分鐘后，時針與分針第一次成90°角，依題意有
6x-0.5x-60=90，
解得x=$\frac{300}{11}$．
故經過$\frac{300}{11}$分鐘后，時針與分針第一次成90°角；
②2時～3時，時針與分針成60°角，
6m-60-0.5m=60，
解得m=$\frac{240}{11}$；
故3時～4時，時針在前面，分針在后面，時針與分針成60°角，
90+0.5n-6n=60，
解得n=$\frac{60}{11}$；
3時～4時，分針在前面，時針在后面，時針與分針成60°角；
6t-90-0.5t=60，
解得t=$\frac{300}{11}$．
故從2點到4點（不含2點）有3次時針與分針成60°角，分別是2時$\frac{240}{11}$分，3時$\frac{60}{11}$分，3時$\frac{300}{11}$分．

點評 本題考查了鐘表問題，解題時經常用到每兩個數字之間的度數是30°，分鐘每分鐘轉過的角度為6度，時鐘每分鐘轉過的角度為0.5度．借助圖形，更容易解決．同時考查一元一次方程的應用，得到時針所走路程和分針所走路程的等量關系是解決本題的關鍵．