
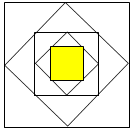
 如圖,把一個正方形各邊中點連結起來組成第二個正方形,再把第二個正方形各邊的中點連結起來組成第三個正方形,按照這樣的方法連結得到的第五個正方形的面積占第一個正方形面積的$\frac{1}{16}$.(填幾分之幾)
如圖,把一個正方形各邊中點連結起來組成第二個正方形,再把第二個正方形各邊的中點連結起來組成第三個正方形,按照這樣的方法連結得到的第五個正方形的面積占第一個正方形面積的$\frac{1}{16}$.(填幾分之幾) 分析 先根據正方形的邊長是1,得出斜邊的長,根據面積公式計算出第二個正方形的面積,以此類推,得出第三個正方形的面積,總結出規律,得到第n個正方形的面積,再把n=5時代入即可求出答案.
解答 解:∵正方形的邊長是1,
所以它的斜邊長是:$\sqrt{({\frac{1}{2})}^{2}+(\frac{1}{2})^{2}}$=$\sqrt{\frac{1}{2}}$,
所以第二個正方形的面積是:$\sqrt{\frac{1}{2}}$×$\sqrt{\frac{1}{2}}$=$\frac{1}{2}$,
第三個正方形的面積為$\frac{1}{4}$=($\frac{1}{2}$)2,
以此類推,第n個正方形的面積為($\frac{1}{2}$)n-1,
所以第五個正方形的面積是($\frac{1}{2}$)5-1=$\frac{1}{16}$;
故答案為$\frac{1}{16}$.
點評 本題考查了正方形的性質以及圖形的變化類,解題的關鍵是掌握中位線定理和正方形的性質,計算出各邊的長,再根據面積公式求出答案.


科目:初中數學 來源: 題型:解答題
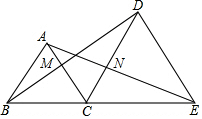 如圖,B,C,E三點在一條直線上,△ABC和△DCE均為等邊三角形,BD與AC交于點M,AE與CD交于點N.
如圖,B,C,E三點在一條直線上,△ABC和△DCE均為等邊三角形,BD與AC交于點M,AE與CD交于點N.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
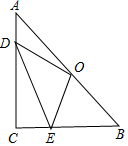 在Rt△ABC中,點O為斜邊AB的中點,D、E分別在邊AC、BC上,若CB=6,CA=8,高CH=$\frac{24}{5}$,則OD+DE+EO的最小值為10.
在Rt△ABC中,點O為斜邊AB的中點,D、E分別在邊AC、BC上,若CB=6,CA=8,高CH=$\frac{24}{5}$,則OD+DE+EO的最小值為10.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com