
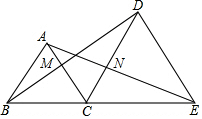
 如圖,B,C,E三點在一條直線上,△ABC和△DCE均為等邊三角形,BD與AC交于點M,AE與CD交于點N.
如圖,B,C,E三點在一條直線上,△ABC和△DCE均為等邊三角形,BD與AC交于點M,AE與CD交于點N.分析 (2)先根據(jù)等邊三角形的性質(zhì)證明△ACE≌△BCD,則∠DBC=∠EAC,再證明△BCM≌△ACN(ASA),所以CM=CN,得△CMN是等邊三角形,根據(jù)內(nèi)錯角相等得MN∥BE;
(2)畫出一個反例圖形即可說明.
解答 證明:(1)如圖1,∵△ABC和△DCE均為等邊三角形,
∴AC=BC,DC=EC,∠ACB=∠DCE=60°,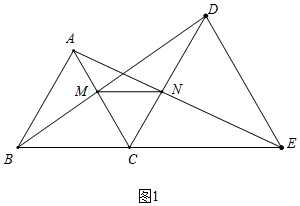
∴∠ACB+∠ACD=∠DCE+∠ACD,∠ACD=180°-60°-60°=60°,
即∠ACE=∠BCD,
在△ACE和△BCD中,
∵$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CE=CD}\end{array}\right.$,
∴△ACE≌△BCD(SAS),
∴∠DBC=∠EAC,
在△BCM和△ACN中,
∵$\left\{\begin{array}{l}{∠DBC=∠EAC}\\{BC=AC}\\{∠ACB=∠ACN=60°}\end{array}\right.$,
∴△BCM≌△ACN(ASA),
∴CM=CN,
∵∠MCN=60°,
∴△CMN是等邊三角形,
∴∠CMN=60°,
∴∠CMN=∠ACB=60°,
∴MN∥BE;
(2)不成立.請看圖2.當M與A重合時,顯然NM與BE相交,不平行.
點評 本題考查等邊三角形的性質(zhì)、全等三角形的判定和性質(zhì)等知識,解題的關(guān)鍵是熟練掌握全等三角形的判定和性質(zhì),學(xué)會利用反例圖形解決問題,屬于中考常考題型.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 32 | B. | 64 | C. | 128 | D. | 16 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | x>1 | B. | x≥0 | C. | x≤0 | D. | x<1 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖所示,△ABC中,AB+BC=10,A、C關(guān)于直線DE對稱,則△BCD的周長是( )
如圖所示,△ABC中,AB+BC=10,A、C關(guān)于直線DE對稱,則△BCD的周長是( )| A. | 6 | B. | 8 | C. | 10 | D. | 無法確定 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
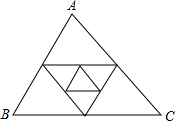 如圖,已知△ABC的周長為1,連結(jié)△ABC三邊的中點構(gòu)成第二個三角形,再連結(jié)第二個三角形三邊的中點構(gòu)成第三個三角形,依此類推,則第2016個三角形的周長為( )
如圖,已知△ABC的周長為1,連結(jié)△ABC三邊的中點構(gòu)成第二個三角形,再連結(jié)第二個三角形三邊的中點構(gòu)成第三個三角形,依此類推,則第2016個三角形的周長為( )| A. | $\frac{1}{2015}$ | B. | $\frac{1}{2016}$ | C. | $\frac{1}{{2}^{2015}}$ | D. | $\frac{1}{{2}^{2016}}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
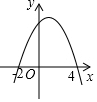 如圖,二次函數(shù)y=ax2+bx+c的圖象與x軸交于(-2,0)和(4,0)兩點,當函數(shù)值y>0時,自變量x的取值范圍是( )
如圖,二次函數(shù)y=ax2+bx+c的圖象與x軸交于(-2,0)和(4,0)兩點,當函數(shù)值y>0時,自變量x的取值范圍是( )| A. | x<-2 | B. | x>4 | C. | -2<x<4 | D. | x>0 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
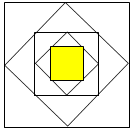 如圖,把一個正方形各邊中點連結(jié)起來組成第二個正方形,再把第二個正方形各邊的中點連結(jié)起來組成第三個正方形,按照這樣的方法連結(jié)得到的第五個正方形的面積占第一個正方形面積的$\frac{1}{16}$.(填幾分之幾)
如圖,把一個正方形各邊中點連結(jié)起來組成第二個正方形,再把第二個正方形各邊的中點連結(jié)起來組成第三個正方形,按照這樣的方法連結(jié)得到的第五個正方形的面積占第一個正方形面積的$\frac{1}{16}$.(填幾分之幾)查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com