
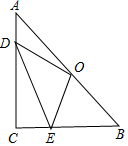
 在Rt△ABC中,點O為斜邊AB的中點,D、E分別在邊AC、BC上,若CB=6,CA=8,高CH=$\frac{24}{5}$,則OD+DE+EO的最小值為10.
在Rt△ABC中,點O為斜邊AB的中點,D、E分別在邊AC、BC上,若CB=6,CA=8,高CH=$\frac{24}{5}$,則OD+DE+EO的最小值為10. 分析 如圖,作點O關于AC的對稱點O′,點O關于BC的對稱點O″,連接O′O″.因為△ODE的周長=OD+DE+OE=O′D+DE+EO″,根據兩點直徑線段最短,可知當O′、D、E、O″共線時,△ODE的周長最小,最小值為O′O″,求出O′O″即可.
解答 解:如圖,作點O關于AC的對稱點O′,點O關于BC的對稱點O″,連接O′O″.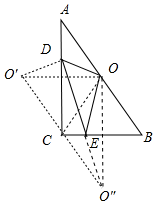
∵△ODE的周長=OD+DE+OE=O′D+DE+EO″,
根據兩點直徑線段最短,可知當O′、D、E、O″共線時,△ODE的周長最小,最小值為O′O″,
∵∠ACB=90°,AC=8,BC=6,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,根據對稱性可知,O′、C、O″共線,
∵AO=OB,
∴OC=$\frac{1}{2}$AB=5,
∴O′O″=2OC=10.
∴OD+DE+EO的最小值為10,
故答案為10.
點評 本題考查軸對稱-最短問題、勾股定理、直角三角形斜邊中線性質等知識,解題的關鍵是學會利用對稱解決最短問題,屬于中考常考題型.


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
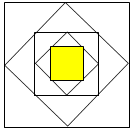 如圖,把一個正方形各邊中點連結起來組成第二個正方形,再把第二個正方形各邊的中點連結起來組成第三個正方形,按照這樣的方法連結得到的第五個正方形的面積占第一個正方形面積的$\frac{1}{16}$.(填幾分之幾)
如圖,把一個正方形各邊中點連結起來組成第二個正方形,再把第二個正方形各邊的中點連結起來組成第三個正方形,按照這樣的方法連結得到的第五個正方形的面積占第一個正方形面積的$\frac{1}{16}$.(填幾分之幾)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com