
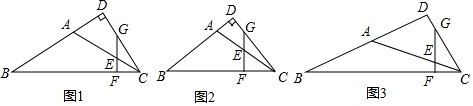
分析 (1)首先證明∠DCA=30°,∠GCF=60°,∠CGF=30°,設EF=a,在Rt△ECF中,CE=2EF=2a,CF=$\sqrt{3}$a,CG=2CF=2$\sqrt{3}$a,由∠EGC=∠ECG=30°,推出EG=EC=2a,推出$\frac{CG}{EG}$=$\frac{2\sqrt{3}a}{2a}$=$\sqrt{3}$,即可證明.
(2)如圖2中,作AM⊥BC于M.由AM∥EF,AE=EC,推出FM=FC,由AB=AC,AM⊥BC,推出BM=CM,BM=2MF,由BF=6$\sqrt{2}$,推出MF=CF=2$\sqrt{2}$,BC=2BM=8$\sqrt{2}$,
由∠DCB=∠GCF,∠GFC=∠BDC=90°,推出△GFC∽△BDC,可得$\frac{CG}{BC}$=$\frac{CF}{CD}$,求出CD即可解決問題.
(3)由△FEC∽△FCG,可得CF2=EF•FG,設EF=a,CF=m,則GE=$\sqrt{2}$m,可得m2=a(a+$\sqrt{2}$m),推出a=$\frac{\sqrt{6}-\sqrt{2}}{2}$m或$\frac{-\sqrt{6}-\sqrt{2}}{2}$m(舍棄),推出tan∠ECF=tan∠B=$\frac{\sqrt{6}-\sqrt{2}}{2}$=$\frac{AM}{BM}$=$\frac{DC}{BD}$,設AM=($\sqrt{6}$-$\sqrt{2}$)k,BM=2k,CD=($\sqrt{6}$-$\sqrt{2}$)n,BD=2n,則BC=4k,在Rt△BDC中,由BD2+CD2=BC2,可得4n2+[($\sqrt{6}$-$\sqrt{2}$)n]2=(4k)2,可得n=$\frac{4k}{\sqrt{12-4\sqrt{3}}}$,推出BD=$\frac{8k}{\sqrt{12-4\sqrt{3}}}$,在Rt△ABM中,AB=$\sqrt{A{M}^{2}+B{M}^{2}}$=$\sqrt{12-4\sqrt{3}}$k,推出AD=BD-AB=$\frac{8k}{\sqrt{12-4\sqrt{3}}}$-$\sqrt{12-4\sqrt{3}}$k,由此即可解決問題.
解答 (1)證明:如圖1中,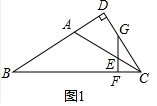
∵AB=AC,∠BAC=120°,
∴∠B=∠ACB=30°,
∴∠DAC=∠B+∠ACB=60°,
∵∠D=∠GFC=90°,
∴∠DCA=30°,∠GCF=60°,∠CGF=30°,設EF=a,
在Rt△ECF中,CE=2EF=2a,CF=$\sqrt{3}$a,CG=2CF=2$\sqrt{3}$a,
∵∠EGC=∠ECG=30°,
∴EG=EC=2a,
∴$\frac{CG}{EG}$=$\frac{2\sqrt{3}a}{2a}$=$\sqrt{3}$,
∴CG=$\sqrt{3}$EG.
(2)解:如圖2中,作AM⊥BC于M.
∵GF⊥BC,
∴AM∥EF,
∵AE=EC,
∴FM=FC,
∵AB=AC,AM⊥BC,
∴BM=CM,BM=2MF,
∵BF=6$\sqrt{2}$,
∴MF=CF=2$\sqrt{2}$,BC=2BM=8$\sqrt{2}$,
∵∠DCB=∠GCF,∠GFC=∠BDC=90°,
∴△GFC∽△BDC,
∴$\frac{CG}{BC}$=$\frac{CF}{CD}$,
∴$\frac{5}{8\sqrt{2}}$=$\frac{2\sqrt{2}}{CD}$,
∴CD=$\frac{32}{5}$,
∴DG=CD-CG=$\frac{32}{5}$-5=$\frac{7}{5}$.
(3)如圖3中,
∵∠B+∠GCF=90°,∠GCF+∠FGC=90°,
∴∠FGC=∠B,
∵∠B=∠ECF,
∴∠ECF=∠FGC,∵∠EFC=∠GFC,
∴△FEC∽△FCG,
∴CF2=EF•FG,設EF=a,CF=m,則GE=$\sqrt{2}$m,
∴m2=a(a+$\sqrt{2}$m),
∴a2+$\sqrt{2}$ma-a2=0,
∴a=$\frac{\sqrt{6}-\sqrt{2}}{2}$m或$\frac{-\sqrt{6}-\sqrt{2}}{2}$m(舍棄),
∴tan∠ECF=tan∠B=$\frac{\sqrt{6}-\sqrt{2}}{2}$=$\frac{AM}{BM}$=$\frac{DC}{BD}$,設AM=($\sqrt{6}$-$\sqrt{2}$)k,BM=2k,CD=($\sqrt{6}$-$\sqrt{2}$)n,BD=2n,則BC=4k,
在Rt△BDC中,∵BD2+CD2=BC2,
∴4n2+[($\sqrt{6}$-$\sqrt{2}$)n]2=(4k)2,
可得n=$\frac{4k}{\sqrt{12-4\sqrt{3}}}$,
∴BD=$\frac{8k}{\sqrt{12-4\sqrt{3}}}$,
在Rt△ABM中,AB=$\sqrt{A{M}^{2}+B{M}^{2}}$=$\sqrt{12-4\sqrt{3}}$k,
∴AD=BD-AB=$\frac{8k}{\sqrt{12-4\sqrt{3}}}$-$\sqrt{12-4\sqrt{3}}$k,
∴$\frac{AD}{AB}$=$\frac{\frac{8k}{\sqrt{12-4\sqrt{3}}}-\sqrt{12-4\sqrt{3}}k}{\sqrt{12-4\sqrt{3}}k}$=$\frac{8}{12-4\sqrt{3}}$-1=$\frac{2}{3-\sqrt{3}}$-1=$\frac{\sqrt{3}}{3}$.
點評 本題考查三角形綜合題、等腰三角形的性質、銳角三角函數、相似三角形的判定和性質、一元二次方程,30度的直角三角形的性質等知識,解題的關鍵是學會添加常用輔助線,構造直角三角形解決問題,學會利用參數解決問題,屬于中考壓軸題.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0.93×109 | B. | 9.3×108 | C. | 9.3×109 | D. | 93×107 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 8.5 | B. | 3.5 | C. | 8.5或3.5 | D. | 8.3或3.7 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
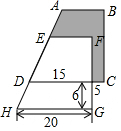 如圖所示,兩個完全相同的直角梯形重疊在一起,將其中一個直角梯形沿AD的方向平移,平移的距離為線段AE的長,求陰影部分的面積.(單位:cm)
如圖所示,兩個完全相同的直角梯形重疊在一起,將其中一個直角梯形沿AD的方向平移,平移的距離為線段AE的長,求陰影部分的面積.(單位:cm)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com