
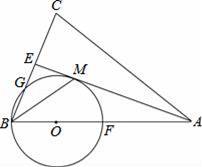
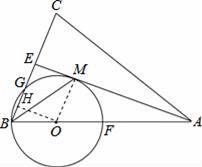
如圖,在△ABC中,AB=AC,AE是∠BAC的平分線,∠ABC的平分線 BM交AE于點M,點O在AB上,以點O為圓心,OB的長為半徑的圓經過點M,交BC于點G,交 AB于點F.
(1)求證:AE為⊙O的切線.
(2)當BC=8,AC=12時,求⊙O的半徑.
(3)在(2)的條件下,求線段BG的長.

【考點】圓的綜合題.
【專題】證明題.
【分析】(1)連接OM.利用角平分線的性質和平行線的性質得到AE⊥OM后即可證得AE是⊙O的切線;
(2)設⊙O的半徑為R,根據OM∥BE,得到△OMA∽△BEA,利用平行線的性質得到
 =
=
 ,即可解得R=3,從而求得⊙O的半徑為3;
,即可解得R=3,從而求得⊙O的半徑為3;
(3)過點O作OH⊥BG于點H,則BG=2BH,根據∠OME=∠MEH=∠EHO=90°,得到四邊形OMEH是矩形,從而得到HE=OM=3和BH=1,證得結論BG=2BH=2.
【解答】(1)證明:連接OM.
∵AC=AB,AE平分∠BAC,
∴AE⊥BC,CE=BE=
 BC=4,
BC=4,
∵OB=OM,
∴∠OBM=∠OMB,
∵BM平分∠ABC,
∴∠OBM=∠CBM,
∴∠OMB=∠CBM,
∴OM∥BC
又∵AE⊥BC,
∴AE⊥OM,
∴AE是⊙O的切線;
(2)設⊙O的半徑為R,
∵OM∥BE,
∴△OMA∽△BEA,
∴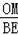
 =
=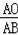
 即
即
 =
=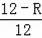
 ,
,
解得R=3,
∴⊙O的半徑為3;
(3)過點O作OH⊥BG于點H,則BG=2BH,
∵∠OME=∠MEH=∠EHO=90°,
∴四邊形OMEH是矩形,
∴HE=OM=3,
∴BH=1,
∴BG=2BH=2.

【點評】本題考查了圓的綜合知識,題目中還運用到了切線的判定與性質、相似三角形的判定與性質,綜合性較強,難度較大.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
在一次消防演習中,消防員架起一架25米長的云梯AB,如圖斜靠在一面墻上,梯子底端B離墻角C的距離為7米.
(1)求這個梯子的頂端距地面AC有多高?
(2)如果消防員接到命令,按要求將梯子底部在水平方向滑動后停在DE的位置上(云梯長度不變),測得BD長為8米,那么云梯的頂部在下滑了多少米?


查看答案和解析>>
科目:初中數學 來源: 題型:
國務院總理李克強在第十二屆全國人大第四次政府工作報告中指出,2015年我國國內生產總值達到了67.7萬億元,67.7萬億元用科學記數法表示為( )
A.67.7×1012 B.6.77×1013 C.0.677×1014 D.6.77×1014
查看答案和解析>>
科目:初中數學 來源: 題型:
下列命題中逆命題是真命題的是( )
A.對頂角相等
B.若兩個角都是45°,那么這兩個角相等
C.全等三角形的對應角相等
D.兩直線平行,同位角相等
查看答案和解析>>
科目:初中數學 來源: 題型:
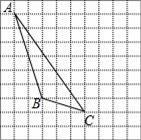
如圖,在方格紙內將△ABC水平向右平移5個單位得到△A′B′C′.
(1)補全△A′B′C′;利用網格點和直尺畫圖:
(2)畫出AB邊上的高線CD;
(3)圖中△ABC的面積是 ;
(4)△ABC與△EBC面積相等,在圖中描出所有滿足條件且異于A點的格點E,并記為E1E2E3.

查看答案和解析>>
科目:初中數學 來源: 題型:
甲乙兩車沿直路同向行駛,車速分別為20m/s和25m/s.現甲車在乙車前500m處,設xs(0≤x≤100)后兩車相距ym.那么y關于x的數解析式為 .(寫出自變量取值范圍)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com