Question

9．如圖，形如量角器的半圓O的直徑DE=12cm，形如三角板的△ABC中，∠ACB=90°，∠ABC=30°，BC=12cm半圓O以2cm/s的速度從左向右運動，在運動過程中，點D、E始終在直線BC上．設運動時間為t（s），當t=0s時，半圓O在△ABC的左側，OC=8cm．
（1）當t=1（s）時，⊙O與AC所在直線第一次相切；點C到直線AB的距離為6；
（2）當t為何值時，直線AB與半圓O所在的圓相切；
（3）當△ABC的一邊所在直線與圓O相切時，若⊙O與△ABC有重疊部分，求重疊部分的面積．

Answer 1

分析 （1）求出路程EC的長，即可以求時間t=1，作C到AB的距離CF，利用直角三角形中30°角所對的直角邊是斜邊的一半可以得：CF=6；
（2）根據C到AB的距離為6cm，圓的半徑為6cm，所以O與C重合，即當O點運動到C點時，半圓O與△ABC的邊AB相切，t=8÷2=4秒；
（3）有兩種情況：
①當半圓O與AB邊相切于F時，如圖2，重疊部分的面積是半圓面積的一半；
②當半圓O與AC相切于C時，如圖4，連接OG，重疊部分的面積是扇形OCG的面積+△BOG的面積．

解答 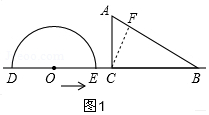解：（1）∵DE=12，
∴OE=OD=6，
∵OC=8，
∴EC=8-6=2，
∴t=2÷2=1，
∴當t=1s時，⊙O與AC所在直線第一次相切；
如圖1，過C作CF⊥AB于F，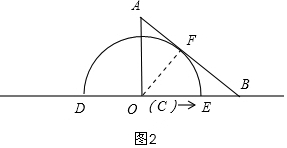
Rt△BCF中，∵∠ABC=30°，BC=12，
∴CF=$\frac{1}{2}$BC=6，
故答案為：1，6；
（2）如圖2，過C作CF⊥AB于F，
同理得：OF=6，
當直線AB與半圓O所在的圓相切時，
又∵圓心O到AB的距離為6，半圓的半徑為6，
且圓心O又在直線BC上，
∴O與C重合，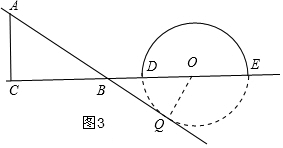
即當O點運動到C點時，半圓O與△ABC的邊AB相切，
此時，點O運動了8cm，所求運動時間t=8÷2=4；
如圖3，當點O運動到B點的右側時，且OB=12，過O作OQ⊥AB，交直線AB于Q，
在Rt△QOB中，∠OBQ=30°，則OQ=$\frac{1}{2}$OB=6，
即OQ與半圓O所在的圓相切，此時點O運動了12+12+8=32cm，
所求運動時間t=32÷2=16，
綜上所述，當t為4秒或16秒時，直線AB與半圓O所在的圓相切；
（3）有兩種情況：
①當半圓O與AB邊相切于F時，如圖2，
重疊部分的面積S=$\frac{1}{4}$π×6²=9π；
②當半圓O與AC相切于C時，如圖4，連接OG，
∵BC=DE=12，
∴C與D重合，E與B重合，
∵OG=OB，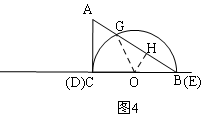
∴∠ABC=∠OGB=30°，
∴∠COG=60°，
過O作OH⊥AB于H，
∵OB=6，
∴OH=$\frac{1}{2}$OB=3，
由勾股定理得：BH=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$，
∴BG=2BH=6$\sqrt{3}$，
此時重疊部分的面積S=$\frac{60π×{6}^{2}}{360}$+$\frac{1}{2}$×$6\sqrt{3}$×3=6π+9$\sqrt{3}$；
綜上所述，重疊部分的面積為9πcm²或（6π+9$\sqrt{3}$）cm²．

點評 本題考查了切線的判定與性質，熟練掌握切線的判定是關鍵：經過半徑的外端且垂直于這條半徑的直線是圓的切線；本題有難度，尤其是第3問，容易漏解，要注意利用數形結合的思想．