Question

14．已知：如圖，在Rt△ABC中，∠ACB=90°，AC=BC，CD⊥AB于點D，點M是AB邊上的點，點N是射線CB上的點，且MC=MN．
（1）如圖1，求證：∠MCD=∠BMN．
（2）如圖2，當點M在∠ACD的平分線上時，請在圖2中補全圖，猜想線段AM與BN有什么數量關系，并證明；
（3）如圖3，當點M是BD中點時，請直接寫出線段AM與BN的數量關系

Answer 1

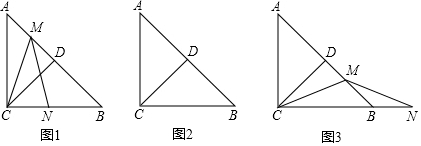
分析 （1）由等腰直角三角形的性質得出∠BCD=∠B=∠A=∠ACD=45°，AD=BD，由等腰三角形的性質得出∠MCN=∠MNC，再由三角形的外角性質即可得出結論；
（2）證出∠ACM=∠BMN，由AAS證明△ACM≌△BMN，得出對應邊相等即可；
（3）作ME⊥BC于E，則△BEM是等腰直角三角形，得出BE=ME，設BE=ME=1，則BM=$\sqrt{2}$BE=$\sqrt{2}$，求出AD=BD=2$\sqrt{2}$，得出AM=3$\sqrt{2}$，由直角三角形斜邊上的中線性質得出CD=$\frac{1}{2}$AB=AD=2$\sqrt{2}$，由勾股定理求出MC=$\sqrt{10}$，NE=CE=$\sqrt{M{C}^{2}-M{E}^{2}}$=3，得出BN=NE-BE=2，即可得出結論．

解答 （1）證明：∵在Rt△ABC中，∠ACB=90°，AC=BC，CD⊥AB，
∴∠BCD=∠B=∠A=∠ACD=45°，AD=BD，
∵MC=MN，
∴∠MCN=∠MNC，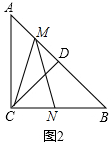
∵∠MCN=∠BCD+∠MCD=45°+∠MCD，∠MNC=∠B+∠BMN，
∴∠MCD=∠BMN．
（2）解：AM=BN；理由如下：如圖2所示：
∵點M在∠ACD的平分線上，
∴∠ACM=∠MCD，
∵∠MCD=∠BMN，
∴∠ACM=∠BMN，
在△ACM和△BMN中，$\left\{\begin{array}{l}{∠A=∠B}&{\;}\\{∠ACM=∠BMN}&{\;}\\{MC=MN}&{\;}\end{array}\right.$，
∴△ACM≌△BMN（AAS），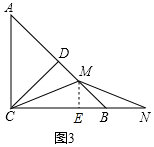
∴AM=BN；
（3）解：2AM=3$\sqrt{2}$BN，理由如下：
作ME⊥BC于E，如圖3所示：
則△BEM是等腰直角三角形，
∴BE=ME，
設BE=ME=1，則BM=$\sqrt{2}$BE=$\sqrt{2}$，
∵點M是BD中點，
∴DM=BM=$\sqrt{2}$，
∴AD=BD=2$\sqrt{2}$，
∴AM=3$\sqrt{2}$，
∵∠ACB=90°，AD=BD，
∴CD=$\frac{1}{2}$AB=AD=2$\sqrt{2}$，
在Rt△DCM中，MC=$\sqrt{C{D}^{2}+D{M}^{2}}$=$\sqrt{10}$，
∵MN=MC，ME⊥BC，
∴NE=CE=$\sqrt{M{C}^{2}-M{E}^{2}}$=$\sqrt{10-1}$=3，
∴BN=NE-BE=2，
∴AM：BN=3$\sqrt{2}$：2，
∴2AM=3$\sqrt{2}$BN．

點評 本題是三角形綜合題目，考查了等腰直角三角形的判定與性質、全等三角形的判定與性質、等腰三角形的性質、勾股定理等知識；熟練掌握等腰直角三角形的判定與性質和全等三角形的判定與性質是解決問題的關鍵．