
分析 (1)由題意,an是相鄰倆奇數2n+1、2n-1的平方差,化簡結果是8的倍數,可整除;
(2)由an=8n找到前四個完全平方數,從下標2、8、18、32可知它們是一個完全平方數的2倍.
解答 解:(1)由題意得:
$\begin{array}{l}{a_n}={(2n+1)^2}-{(2n-1)^2}\\ \;\;\;\;=4{n^2}+4n+1-(4{n^2}-4n+1)\\ \;\;\;\;=8n\end{array}$
∴an能被8整除.
(2)由(1)知an=8n,
當n=2時,${a}_{2}=16={4}^{2},是完全平方數$;
當n=8時,${a}_{8}=64={8}^{2},是完全平方數$;
當n=18時,${a}_{18}=144=1{2}^{2},是完全平方數$;
當n=32時,${a}_{32}=256=1{6}^{2},是完全平方數$.
這一系列數中從小到大排列的前4個完全平方數依次為:16、64、144、256.
由a2、a8、a18、a32四個完全平方數可知n=2×m2,
所以n為一個完全平方數兩倍時,an是完全平方數.
點評 本題主要考查了數字的變化規律,利用代數式來表示一般規律,利用已總結的規律進一步探索、發現、歸納得出下一步結論是本題難點.


 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在邊長為1的小正方形組成的網格中,A、B兩點均在格點上,且坐標分別為A(3,2);B(1,3).
如圖,在邊長為1的小正方形組成的網格中,A、B兩點均在格點上,且坐標分別為A(3,2);B(1,3).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
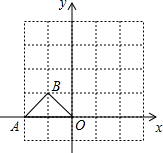 如圖,在平面直角坐標系中,△AOB的頂點A(-2,0)、B(-1,1).將△AOB繞點O順時針旋轉90°后,點A、B分別落在A′、B′.
如圖,在平面直角坐標系中,△AOB的頂點A(-2,0)、B(-1,1).將△AOB繞點O順時針旋轉90°后,點A、B分別落在A′、B′.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
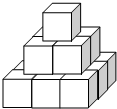 如圖,把14個棱長為1cm的正方體木塊,在地面上堆成如圖所示的立體圖形,然后向露出的表面部分噴漆,若1cm2需用漆2g,那么共需用漆84g.
如圖,把14個棱長為1cm的正方體木塊,在地面上堆成如圖所示的立體圖形,然后向露出的表面部分噴漆,若1cm2需用漆2g,那么共需用漆84g.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,△ABC中,AB=AC,AE是外角∠CAD的平分線,點F在AC上,連結BF并延長與AE交于點E.
如圖,△ABC中,AB=AC,AE是外角∠CAD的平分線,點F在AC上,連結BF并延長與AE交于點E. 查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com