

分析 (1)直接解一元二次方程即可得出點A,B坐標;
(2)先求出∠CBH=30°,進而判斷只有△CHF∽△HBF即可得出FH⊥BC,再求出直線BC解析式,進而得出FH的解析式,聯立直線OC的解析式即可得出結論;
(3)先判斷出∠ACB是直角,即可用直角三角形斜邊的中線等于斜邊的一半即可得出點P的坐標.
解答 解:(1)∵x1,x2是方程x2-8x+12=0的兩根,
∴x1=2,x2=6,∴A(2,0),B(6,0);
(2)存在,理由:如圖1,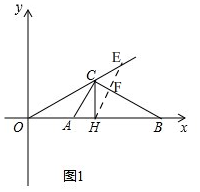 由(1)知,B(6,0),
由(1)知,B(6,0),
∵CH⊥AB于H且C(3,$\sqrt{3}$),
∴H(3,0),
∴OH=BH=3,
∵CH=$\sqrt{3}$,在Rt△BCH中,tan∠CBH=$\frac{CH}{BH}=\frac{\sqrt{3}}{3}$,
∴∠CBH=30°,
∴∠BCH=60°,
∵點E在OC延長線上,
∴∠CHF<60°,
∵△CHF與△BEF相似,
∴△CHF∽△HBF,
∴∠BHF=∠BCH=60°,
∴∠BHF+∠CBH=90°,
∴∠BFH=90°,
∴FH⊥BC,
∵B(6,0),C(3,$\sqrt{3}$),
∴直線BC解析式為y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$,
∵H(3,0),
∴直線FH的解析式為y=$\sqrt{3}$x-3$\sqrt{3}$①,
∵C(3,$\sqrt{3}$),
∴直線OC的解析式為y=$\frac{\sqrt{3}}{3}$x②,
聯立①②得,點E($\frac{9}{2}$,$\frac{3\sqrt{3}}{2}$),
∴OE=3$\sqrt{3}$;
(3)如圖2. ∵A(2,0),B(6,0),C(3,$\sqrt{3}$),
∵A(2,0),B(6,0),C(3,$\sqrt{3}$),
∴AC2+BC2=4+12=16=AB2,
∴△ABC是直角三角形,即:∠ACB=90°,
∵點D是AB中點,
∴D(4,0),CD=$\frac{1}{2}$AB=2,
∵△ABP是直角三角形,
∴∠APB=90°,
①點P和點C重合,即:P(3,$\sqrt{3}$);
②∵∠APB=90°,
∴PD=$\frac{1}{2}$AB=2,
∵P在CD上,
∴D點D也是CP的中點,
∴P(5,-$\sqrt{3}$);
即:滿足條件的點P(3,$\sqrt{3}$)或(5,-$\sqrt{3}$).
點評 此題是相似形綜合題,主要考查了一元二次方程的解法,銳角三角函數,直角三角形的判定和性質,相似三角形的性質,解(2)的關鍵是判斷出△CHF∽△HBF,解(3)的關鍵是得出∠ACB=90°.


科目:初中數學 來源: 題型:填空題
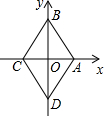 菱形ABCD在直角坐標系中的位置如圖所示,其中點A的坐標為(1,0),點B的坐標為(0,$\sqrt{3}$),動點P從點A出發,沿A→B→C→D→A→B→…的路徑,在菱形的邊上以每秒1個單位長度的速度移動,移動到第2015秒時,點P的坐標為( $\frac{3}{4}$,-$\frac{\sqrt{3}}{4}$).
菱形ABCD在直角坐標系中的位置如圖所示,其中點A的坐標為(1,0),點B的坐標為(0,$\sqrt{3}$),動點P從點A出發,沿A→B→C→D→A→B→…的路徑,在菱形的邊上以每秒1個單位長度的速度移動,移動到第2015秒時,點P的坐標為( $\frac{3}{4}$,-$\frac{\sqrt{3}}{4}$).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
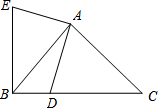
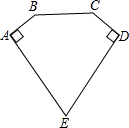 如圖,已知AE=DE=5,AB=CD,BC=4,∠E=60°,∠A=∠D=90°,那么五邊形ABCDE的面積是( )
如圖,已知AE=DE=5,AB=CD,BC=4,∠E=60°,∠A=∠D=90°,那么五邊形ABCDE的面積是( )| A. | 6$\sqrt{2}$ | B. | 6$\sqrt{3}$ | C. | 7$\sqrt{2}$ | D. | 7$\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
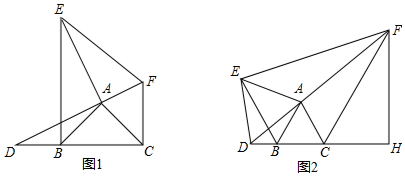
 在等腰 Rt△ABC中,∠A=90°,AC=AB=2,D是BC邊上的點且BD=$\frac{1}{3}$CD,連接AD.AD⊥AE,AE=AD,連接BE.下列結論:
在等腰 Rt△ABC中,∠A=90°,AC=AB=2,D是BC邊上的點且BD=$\frac{1}{3}$CD,連接AD.AD⊥AE,AE=AD,連接BE.下列結論:| A. | 2個 | B. | 3個 | C. | 4個 | D. | 5個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a>0,△>0 | B. | a>0,△<0 | C. | a<0,△>0 | D. | a<0,△<0 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知直線m的解析式為y=-$\frac{1}{2}$x+1,與x軸、y軸分別交于A,B兩點,以線段AB為直角邊在第一象限內作等腰Rt△ABC,且∠BAC=90°,點P為直線x=1上的動點,且△ABP的面積與△ABC的面積相等.
如圖,已知直線m的解析式為y=-$\frac{1}{2}$x+1,與x軸、y軸分別交于A,B兩點,以線段AB為直角邊在第一象限內作等腰Rt△ABC,且∠BAC=90°,點P為直線x=1上的動點,且△ABP的面積與△ABC的面積相等.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com