Question

1．如圖，平行四邊形ABCD在平面直角坐標系中，AD=6，若OA、OB的長是關于x的一元二次方程x²-7x+12=0的兩個根，且OA＞OB
（1）求cos∠ABC的值．
（2）若E為x軸上的點，且S_△AOE=$\frac{16}{3}$，求出點E的坐標，并判斷△AOE與△DAO是否相似？請說明理由．

Answer 1

分析 （1）用因式分解法解出一元二次方程，求出OA、OB的長，即可求得cos∠ABC的值；
（2）設點E的坐標為（m，0），根據三角形的面積公式求出m的值，得到點E的坐標；再求出$\frac{OA}{DA}$和$\frac{OE}{OA}$的值，根據兩組對應邊成比例并且夾角相等的兩個三角形相似證明結論．

解答 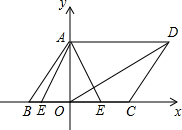解：（1）x²-7x+12=0，
（x-3）（x-4）=0，
解得x₁=3，x₂=4，
∴OA=4，OB=3，
∴Rt△AOB中，AB=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∴cos∠ABC=$\frac{OB}{AB}$=$\frac{3}{5}$；

（2）設點E的坐標為（m，0），則
$\frac{1}{2}$×|m|×4=$\frac{16}{3}$，
解得m=±$\frac{8}{3}$，
∴點E的坐標為：（$\frac{8}{3}$，0）或（-$\frac{8}{3}$，0）；

△AOE∽△DAO．
理由：∵$\frac{OE}{OA}$=$\frac{2}{3}$，=$\frac{OA}{AD}$=$\frac{2}{3}$，
∴$\frac{OE}{OA}$=$\frac{OA}{AD}$，
又∵∠AOE=∠DAO=90°，
∴△AOE∽△DAO．

點評 本題屬于四邊形綜合題，主要考查的是一元二次方程的解法、解直角三角形以及相似三角形的判定的綜合應用，掌握因式分解法解一元二次方程和相似三角形的判定定理是解題的關鍵．