
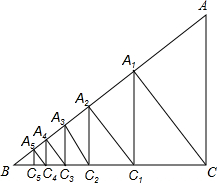
 如圖,已知Rt△ABC中,AC=3,BC=4,過直角頂點C作CA1⊥AB,垂足為A1,再過A1作A1C1⊥BC,垂足為C1,過C2作C2A2⊥AB,垂足為A2,再過A3作A3C3⊥BC,垂足為C3,…,這樣一直做下去,得到了一組線段CA1,A1C1,C2A2,…,則$\frac{{C}_{n-1}{A}_{n}}{{A}_{n}{C}_{n}}$=$\frac{5}{4}$.
如圖,已知Rt△ABC中,AC=3,BC=4,過直角頂點C作CA1⊥AB,垂足為A1,再過A1作A1C1⊥BC,垂足為C1,過C2作C2A2⊥AB,垂足為A2,再過A3作A3C3⊥BC,垂足為C3,…,這樣一直做下去,得到了一組線段CA1,A1C1,C2A2,…,則$\frac{{C}_{n-1}{A}_{n}}{{A}_{n}{C}_{n}}$=$\frac{5}{4}$. 分析 由題意可知:CA1∥C1A2∥…Cn-1An,所以△CA1C1∽△C1A2C2∽…∽△Cn-1AnCn∽△ABC,可知$\frac{{C}_{n-1}{A}_{n}}{{A}_{n}{C}_{n}}$=$\frac{C{A}_{1}}{{A}_{1}{C}_{1}}$=$\frac{AB}{BC}$
解答 解:由題意可知:CA1∥C1A2∥…Cn-1An
∴△CA1C1∽△C1A2C2∽…∽△Cn-1AnCn∽△ABC
∴$\frac{{C}_{n-1}{A}_{n}}{{A}_{n}{C}_{n}}$=$\frac{C{A}_{1}}{{A}_{1}{C}_{1}}$=$\frac{AB}{BC}$
由勾股定理可知:AB=5,
∴$\frac{{C}_{n-1}{A}_{n}}{{A}_{n}{C}_{n}}$=$\frac{AB}{BC}$=$\frac{5}{4}$
故答案為:$\frac{5}{4}$
點評 本題考查相似三角形的性質與判定,考查學生的化歸思想,以及考查學生的觀察能力.


 精英口算卡系列答案
精英口算卡系列答案 應用題點撥系列答案
應用題點撥系列答案 狀元及第系列答案
狀元及第系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
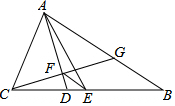 如圖,在△ABC中,AB=5,AC=3,AD、AE分別是其角平分線和中線,過點C作CG⊥AD于F,交AB于G,連接EF,則線段EF的長為1.
如圖,在△ABC中,AB=5,AC=3,AD、AE分別是其角平分線和中線,過點C作CG⊥AD于F,交AB于G,連接EF,則線段EF的長為1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com