
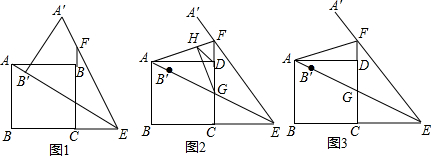
分析 (1)根據(jù)DF=FG-DG,求出DG、DG的長即解決問題.
(2)如圖2中,作AM⊥EF于M,HN⊥CF于N,HJ⊥AD于J.首先證明∠HAG=45°,四邊形HJDN是正方形,設(shè)邊長為b,正方形ABC的邊長為2a,則DG=a,AJ=GN=a+b=2a-b,推出a=2b,求出CE、DH用b表示,即可解決問題.
(3)結(jié)論:EF2=CE2+$\frac{8}{5}$AF2.由(2)可知,tan∠HGN=tan∠FAD=$\frac{HN}{NG}$=$\frac{b}{3b}$=$\frac{1}{3}$,求出DF、AF的長,以及CF與AF的關(guān)系,在Rt△EFC中,根據(jù)EF2=EC2+CF2,即可解決問題.
解答 (1)解:如圖1中,
∵四邊形ABCD是正方形,
∴AB=BC=CD=AD=1,∠B=∠BCD=∠DCE=90°,
∵∠AEB=∠A′EA=30°,
∴BE=$\sqrt{3}$AB=$\sqrt{3}$,EC=BE-BC=$\sqrt{3}-1$,
∴CG=EC•tan30°=1-$\frac{\sqrt{3}}{3}$,GE=2GC=2-$\frac{2\sqrt{3}}{3}$,DG=CD-CG=$\frac{\sqrt{3}}{3}$,
∵∠CGE=∠A′EA+∠GFE=60°,
∴∠GFE=∠GEF=30°,
∴FG=GE=2-$\frac{2\sqrt{3}}{3}$,
∴DF=GF-DG=2-$\frac{2\sqrt{3}}{3}$-$\frac{\sqrt{3}}{3}$=2-$\sqrt{3}$.
(2)證明:如圖2中,作AM⊥EF于M,HN⊥CF于N,HJ⊥AD于J.
∵AD∥BE,
∴∠DAG=∠BEG=∠AEF,
∵AB⊥BE,AM⊥EM,
∴AB=AM=AD,
在Rt△AFM和Rt△AFD中,
$\left\{\begin{array}{l}{AF=AF}\\{AM=AD}\end{array}\right.$,
∴Rt△AFM≌Rt△AFD,
∴∠MAF=∠FAD,
∵∠MAE+∠MEA=90°,
∴2∠FAD+2∠DAG=90°,
∴∠FAD+∠DAG=45°,
∴∠HAG=45°,
∵GH⊥AF,
∴∠HAG=∠HGA=45°,
∴AH=GH,
∵∠FAD+∠AFD=90°∠HGF+∠HFG=90°,
∴∠HAJ=∠HGN,
∴△AHJ≌△GHN,
∴JH=HN,
∵四邊形HJDN是矩形,
∴四邊形HJDN是正方形,設(shè)邊長為b,正方形ABC的邊長為2a,則DG=a,AJ=GN=a+b=2a-b,
∴a=2b,
∵AD∥CE,
∴$\frac{AD}{CE}$=$\frac{DG}{GC}$,
∵DG=GC,
∴AD=CE=2a=4b,
∵DH=$\sqrt{2}$b,
∴b=$\frac{\sqrt{2}}{2}$DH,
∴CE=4•$\frac{\sqrt{2}}{2}$DH=2$\sqrt{2}$DH.
(3)解:結(jié)論:EF2=CE2+$\frac{8}{5}$AF2.理由如下,
如圖3中,由(2)可知,tan∠HGN=tan∠FAD=$\frac{HN}{NG}$=$\frac{b}{3b}$=$\frac{1}{3}$,
∴DF=$\frac{1}{3}$AD=$\frac{4}{3}$b,
AF=$\sqrt{A{D}^{2}+D{F}^{2}}$=$\sqrt{(4b)^{2}+(\frac{4}{3}b)^{2}}$=$\frac{4}{3}$$\sqrt{10}$b,
∴b=$\frac{3AF}{4\sqrt{10}}$,
∵CF=DF+CD=4b+$\frac{4}{3}$b=$\frac{16}{3}$b=$\frac{4}{\sqrt{10}}$AF,
在Rt△EFC中,∵EF2=EC2+CF2,
∴EF2=CE2+($\frac{4}{\sqrt{10}}AF$)2,
∴EF2=CE2+$\frac{8}{5}$AF2.
點(diǎn)評(píng) 本題考查正方形的性質(zhì)、全等三角形的判定和性質(zhì)、四點(diǎn)共圓等知識(shí),解題的關(guān)鍵是添加輔助線構(gòu)造全等三角形,學(xué)會(huì)利用參數(shù),構(gòu)建方程解決問題.屬于中考常考題型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
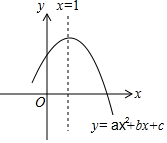 如圖是二次函數(shù)y=ax2+bx+c的圖象,圖象過點(diǎn)A(3,0),對(duì)稱軸為直線x=1,給出以下結(jié)論:①abc<0;②b2-4ac>0;③a-b+c=0;④若B(m2+1,y1)、C(m2+2,y2)為函數(shù)圖象上的兩點(diǎn),則y1<y2;⑤當(dāng)-1≤x≤3時(shí),y≥0.其中正確的結(jié)論是①②③⑤.(填寫正確結(jié)論的序號(hào))
如圖是二次函數(shù)y=ax2+bx+c的圖象,圖象過點(diǎn)A(3,0),對(duì)稱軸為直線x=1,給出以下結(jié)論:①abc<0;②b2-4ac>0;③a-b+c=0;④若B(m2+1,y1)、C(m2+2,y2)為函數(shù)圖象上的兩點(diǎn),則y1<y2;⑤當(dāng)-1≤x≤3時(shí),y≥0.其中正確的結(jié)論是①②③⑤.(填寫正確結(jié)論的序號(hào))查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
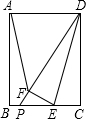 如圖,在矩形ABCD中,AB=6,BC=4,點(diǎn)E是邊BC上一動(dòng)點(diǎn),把△DCE沿DE折疊得△DFE,射線DF交直線CB于點(diǎn)P,當(dāng)△AFD為等腰三角形時(shí),DP的長為$\frac{9}{2}$$\sqrt{2}$或$\frac{24}{7}\sqrt{7}$.
如圖,在矩形ABCD中,AB=6,BC=4,點(diǎn)E是邊BC上一動(dòng)點(diǎn),把△DCE沿DE折疊得△DFE,射線DF交直線CB于點(diǎn)P,當(dāng)△AFD為等腰三角形時(shí),DP的長為$\frac{9}{2}$$\sqrt{2}$或$\frac{24}{7}\sqrt{7}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
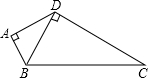 如圖,在四邊形ABCD中,∠A=90°,∠BDC=90°,AD=2,∠ADB=∠C,則點(diǎn)D到BC邊的距離等于2.
如圖,在四邊形ABCD中,∠A=90°,∠BDC=90°,AD=2,∠ADB=∠C,則點(diǎn)D到BC邊的距離等于2.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
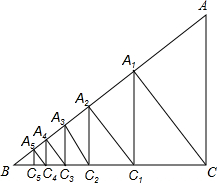 如圖,已知Rt△ABC中,AC=3,BC=4,過直角頂點(diǎn)C作CA1⊥AB,垂足為A1,再過A1作A1C1⊥BC,垂足為C1,過C2作C2A2⊥AB,垂足為A2,再過A3作A3C3⊥BC,垂足為C3,…,這樣一直做下去,得到了一組線段CA1,A1C1,C2A2,…,則$\frac{{C}_{n-1}{A}_{n}}{{A}_{n}{C}_{n}}$=$\frac{5}{4}$.
如圖,已知Rt△ABC中,AC=3,BC=4,過直角頂點(diǎn)C作CA1⊥AB,垂足為A1,再過A1作A1C1⊥BC,垂足為C1,過C2作C2A2⊥AB,垂足為A2,再過A3作A3C3⊥BC,垂足為C3,…,這樣一直做下去,得到了一組線段CA1,A1C1,C2A2,…,則$\frac{{C}_{n-1}{A}_{n}}{{A}_{n}{C}_{n}}$=$\frac{5}{4}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
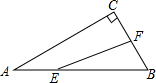 如圖,在△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F(xiàn)是BC的中點(diǎn).若動(dòng)點(diǎn)E以2cm/s的速度從A點(diǎn)出發(fā),沿著A→B→A的方向運(yùn)動(dòng),設(shè)運(yùn)動(dòng)時(shí)間為t(s)(0≤t≤3),連接EF,當(dāng)t為1s或3s或$\frac{7}{4}$s或$\frac{9}{4}$s時(shí),△BEF是直角三角形.
如圖,在△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F(xiàn)是BC的中點(diǎn).若動(dòng)點(diǎn)E以2cm/s的速度從A點(diǎn)出發(fā),沿著A→B→A的方向運(yùn)動(dòng),設(shè)運(yùn)動(dòng)時(shí)間為t(s)(0≤t≤3),連接EF,當(dāng)t為1s或3s或$\frac{7}{4}$s或$\frac{9}{4}$s時(shí),△BEF是直角三角形.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
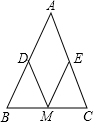 如圖,已知:△ABC中,AB=AC,M、D、E分別是BC、AB、AC的中點(diǎn).
如圖,已知:△ABC中,AB=AC,M、D、E分別是BC、AB、AC的中點(diǎn).查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com