
分析 根據(jù)AF的不確定,分兩種情況:
①當(dāng)AF在AE的右側(cè)時,如圖1,證明△ABH≌△ADG和△AHE≌△AGE,得EG=EH,設(shè)DG=x,在Rt△ECG中,利用勾股定理列方程解出即可,最后再利用勾股定理求DF的長;
②當(dāng)AF在AE的左側(cè)時,如圖2,設(shè)BF=x,同理可求出x的值,同理可利用勾股定理求DF的長.
解答 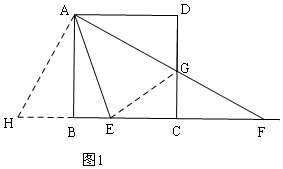 解:分兩種情況:
解:分兩種情況:
①當(dāng)AF在AE的右側(cè)時,如圖1,
延長CB至H,使BH=DG,連接AH,
∵四邊形ABCD為正方形,
∴AB=AD,∠ABC=∠ADC=90°,
∴∠ABH=∠ADC=90°,
∴△ABH≌△ADG,
∴∠HAB=∠GAD,AG=AH,
∵∠EAF=45°,∠BAD=90°,
∴∠BAE+∠GAD=∠BAE+∠HAB=45°,
即∠HAE=45°,
∴∠HAE=∠EAF,
∵AE=AE,
∴△AHE≌△AGE,
∴EG=EH,
設(shè)DG=x,則CG=6-x,EG=EH=2+x,
∵BC=6,BE=2,
∴EC=4,
由勾股定理得:(2+x)2=(6-x)2+42,
x=3,
∴CG=6-x=6-3=3,
∵四邊形ABCD為正方形,
∴CG∥AB,
∴△GCF∽△ABF,
∴$\frac{GC}{AB}=\frac{CF}{BF}$,
∴$\frac{3}{6}$=$\frac{CF}{CF+6}$,
∴CF=6
在Rt△DCF中,由勾股定理得:DF=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$,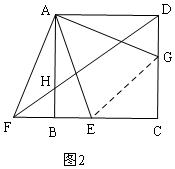
②當(dāng)AF在AE的左側(cè)時,如圖2,
設(shè)BF=x,
在DC上截取DG=BF=x,連接AG、EG,
則CG=6-x,
同理得:△AEF≌△AEG,
∴EG=EF=2+x,
在Rt△ECG中,由勾股定理得:(2+x)2=(6-x)2+42,
x=3,
∴FC=BF+BC=3=6=9,
在Rt△DFC中,DF=$\sqrt{{6}^{2}+{9}^{2}}$=3$\sqrt{13}$,
綜上所述,DF的長為6$\sqrt{2}$或3$\sqrt{13}$;
故答案為:6$\sqrt{2}$或3$\sqrt{13}$.
點評 本題考查了正方形的性質(zhì)、全等三角形的性質(zhì)和判定,本題輔助線的作法是關(guān)鍵,利用輔助線構(gòu)建全等三角形,并采用了分類討論的思想,本題容易丟解,要注意利用數(shù)形結(jié)合的思想,解決問題.


 口算題天天練系列答案
口算題天天練系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 3個 | B. | 2個 | C. | 1 | D. | 0個 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2、3、$\sqrt{5}$ | B. | 8、15、17 | C. | 0.6、0.8、1 | D. | $\sqrt{5}$、$\sqrt{12}$、$\sqrt{13}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 將長為30cm寬為10cm的長方形白紙,按如圖方法粘合起來,粘合部分的寬度為3cm
將長為30cm寬為10cm的長方形白紙,按如圖方法粘合起來,粘合部分的寬度為3cm查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com