
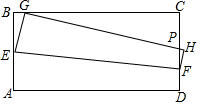
 在矩形紙片ABCD中,AB=2,BC=4,E為AB上一點,F為CD上一點.將矩形紙片沿EF折疊,使得點A恰落在線段BC上,標為點G.
在矩形紙片ABCD中,AB=2,BC=4,E為AB上一點,F為CD上一點.將矩形紙片沿EF折疊,使得點A恰落在線段BC上,標為點G.分析 (1)如圖1,利用勾股定理在Rt△BEG中列式可求得y關于x的關系式;如圖2時,當F與D重合時,BG的值最大,
求出此時的最大值為:x=AE=4-2$\sqrt{3}$,寫出結論;
(2)證明△BEG∽△CGP和△BEG∽△HFP,列比例式,再把y=$\frac{1}{4}{x}^{2}$+1代入即可得出z關于x的關系式;
(3)由∠PMD=30°,可依次推得:∠BEG=30°,則EG=2BG,即y=2x,得方程為:$\frac{1}{4}{x}^{2}$+1=2x,解出即可.
解答 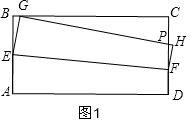 解:(1)如圖1,由折疊得:EG=AE=y,則BE=2-y,
解:(1)如圖1,由折疊得:EG=AE=y,則BE=2-y,
∵四邊形ABCD為矩形,
∴∠B=90°,
由勾股定理得:EG2=BE2+BG2,
y2=(2-y)2+x2,
∴y=$\frac{1}{4}{x}^{2}$+1,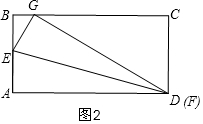
如圖2,當F與D重合時,BG的值最大,
由折疊得:DG=AB=4,
在Rt△DGC中,DC=2,
CG=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴x=AE=4-2$\sqrt{3}$,
∴y關于x的關系式為:y=$\frac{1}{4}{x}^{2}$+1(0≤x≤4-2$\sqrt{3}$);
(2)如圖1,∵∠EGP=90°,
∴∠BGE+∠PGC=90°,
∵∠B=90°,
∴∠BGE+∠BEG=90°,
∴∠PGC=∠BEG,
∵∠B=∠C=90°,
∴△BEG∽△CGP,
∴$\frac{BG}{CP}=\frac{BE}{CG}$,
∴$\frac{x}{CP}=\frac{2-y}{4-x}$,
∴CP=$\frac{x(4-x)}{2-y}$,
∴FP=CD-DF-CP=2-z-$\frac{x(4-x)}{2-y}$,
同理得:△BEG∽△HFP,
∴$\frac{BE}{HF}=\frac{EG}{FP}$,
∴BE•FP=FH•EG,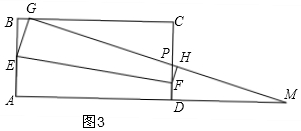
∴(2-y)•[2-z-$\frac{x(4-x)}{2-y}$]=yz,
z=$\frac{1}{4}{x}^{2}-2x+1$;
(3)存在,使直線GP和直線AD的夾角為30°,如圖3,
∵∠PMD=30°,
∴∠DPM=60°,
∴∠GPC=∠DPM=60°,
∵∠C=90°,
∴∠PGC=30°,
∵∠EGP=90°,
∴∠BGE=60°,
∴∠BEG=30°,
∴EG=2BG,
即y=2x,
由(1)得:y=$\frac{1}{4}{x}^{2}$+1,
∴$\frac{1}{4}{x}^{2}$+1=2x,
解得:x1=4+2$\sqrt{3}$>4(不符合題意,舍),x2=4-2$\sqrt{3}$,
∴當x=4-2$\sqrt{3}$時,直線GP和直線AD的夾角為30°.
點評 本題是四邊形的綜合題,考查了矩形、折疊的性質、相似三角形的性質和判定、勾股定理;熟練掌握折疊前后的兩邊相等,兩角相等,利用相似列比例式或利用勾股定理列等式,與方程相結合,列函數關系式或一元二次方程求解.


 同步輕松練習系列答案
同步輕松練習系列答案 課課通課程標準思維方法與能力訓練系列答案
課課通課程標準思維方法與能力訓練系列答案科目:初中數學 來源: 題型:填空題
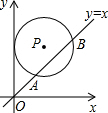 如圖,在平面直角坐標系中,⊙P的圓心坐標是(4,a)(a>4),半徑為4,函數y=x的圖象被⊙P截得的弦AB的長為4$\sqrt{3}$,則a的值是4+2$\sqrt{2}$.
如圖,在平面直角坐標系中,⊙P的圓心坐標是(4,a)(a>4),半徑為4,函數y=x的圖象被⊙P截得的弦AB的長為4$\sqrt{3}$,則a的值是4+2$\sqrt{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
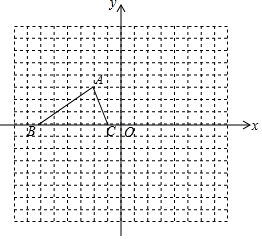 如圖,已知△ABC的三個頂點的坐標分別為A(-2,3),B(-6,0),C(-1,0).
如圖,已知△ABC的三個頂點的坐標分別為A(-2,3),B(-6,0),C(-1,0).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
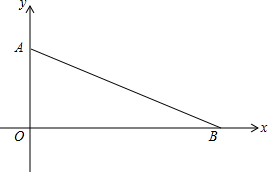 如圖,在平面直角坐標系中,點A(0,7),B(24,0).△AOB內是否有一點P到各邊的距離相等?如果有,請作出這一點,并求出符合條件的點P的坐標.
如圖,在平面直角坐標系中,點A(0,7),B(24,0).△AOB內是否有一點P到各邊的距離相等?如果有,請作出這一點,并求出符合條件的點P的坐標.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1組 | B. | 3組 | C. | 4組 | D. | 7組 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com