
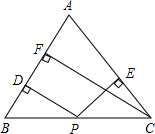
 如圖所示,在等腰三角形ABC中.底邊BC上有任意一點P,則點P到兩腰的距離之和等于定長(腰上的高),即PD+PE=CF,若點P在BC的延長線上,那么PD,PE和CF存在什么等式關系?寫出你的猜想并加以證明.(提示:有三個角等于90°的四邊形是長方形.)
如圖所示,在等腰三角形ABC中.底邊BC上有任意一點P,則點P到兩腰的距離之和等于定長(腰上的高),即PD+PE=CF,若點P在BC的延長線上,那么PD,PE和CF存在什么等式關系?寫出你的猜想并加以證明.(提示:有三個角等于90°的四邊形是長方形.) 分析 先過點C作CG⊥PD于G,構造矩形CFDG,得出CF=DG,再判定△PCG≌△PCE(AAS),得出PG=PE,進而得到PD=DG+PG=CF+PE.
解答  解:PD=CF+PE.
解:PD=CF+PE.
證明:如圖所示,過點C作CG⊥PD于G,則∠CGD=90°,
∵CF⊥AB,PD⊥AB,
∴∠CFD=∠GDF=90°,
∴四邊形CFDG是長方形,
∴CF=DG,
∵AB=AC,
∴∠B=∠ACB,
又∵CG∥AB,
∴∠PCG=∠B,
又∵∠ACB=∠PCE,
∴∠PCG=∠PCE,
∵PE⊥AE,
∴∠PGC=∠E=90°,
在△PCG和△PCE中,
$\left\{\begin{array}{l}{∠PGC=∠E}\\{∠PCG=∠PCE}\\{CP=CP}\end{array}\right.$,
∴△PCG≌△PCE(AAS),
∴PG=PE,
∴PD=DG+PG=CF+PE.
點評 本題主要考查了矩形的判定與全等三角形的判定與性質的綜合應用,解決問題的關鍵是作輔助線構造矩形和全等三角形,根據矩形對邊相等以及全等三角形對應邊相等計算推導.


科目:初中數學 來源: 題型:解答題
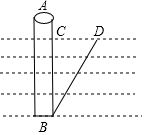 橋梁工程師想探知50m高的一根橋樁是否與地面垂直,他用鉛錘系著一根與橋樁等長的繩子沉到橋樁底部,這時發現水面向上露出10m(AC),再斜拉繩子的端點A到水面的D處,測得CD=30m,根據這位工程師測得的數據,判斷橋樁與地面是否垂直.
橋梁工程師想探知50m高的一根橋樁是否與地面垂直,他用鉛錘系著一根與橋樁等長的繩子沉到橋樁底部,這時發現水面向上露出10m(AC),再斜拉繩子的端點A到水面的D處,測得CD=30m,根據這位工程師測得的數據,判斷橋樁與地面是否垂直.查看答案和解析>>
科目:初中數學 來源:2017屆江蘇省無錫市九年級下學期第一次模擬考試數學試卷(解析版) 題型:解答題
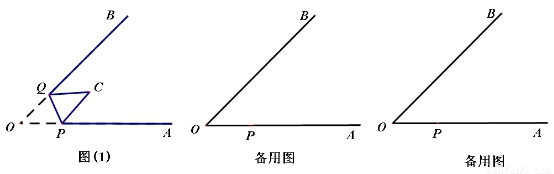
如圖(1),∠AOB=45°,點P、Q分別是邊OA,OB上的兩點,且OP=2cm.將∠O沿PQ折疊,點O落在平面內點C處.
(1)①當PC∥QB時,OQ= ;
②當PC⊥QB時,求OQ的長.
(2)當折疊后重疊部分為等腰三角形時,求OQ的長.
查看答案和解析>>
科目:初中數學 來源:2017屆江蘇省無錫市九年級下學期第一次模擬考試數學試卷(解析版) 題型:單選題
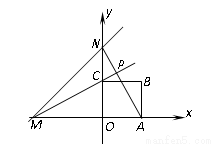
直線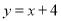 分別與x軸、y軸相交與點M、N,邊長為2的正方形OABC一個頂點O在坐標系的原點,直線AN與MC相交與點P,若正方形繞著點O旋轉一周,則點P到點(0,2)長度的最小值是( )
分別與x軸、y軸相交與點M、N,邊長為2的正方形OABC一個頂點O在坐標系的原點,直線AN與MC相交與點P,若正方形繞著點O旋轉一周,則點P到點(0,2)長度的最小值是( )
A.  B.
B. 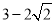 C.
C. 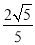 D. 1
D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com