
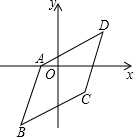
 如圖,已知?ABCD三個頂點坐標(biāo)是A(-1,0)、B(-2,-3)、C(2,-1),那么第四個頂點D的坐標(biāo)是( )
如圖,已知?ABCD三個頂點坐標(biāo)是A(-1,0)、B(-2,-3)、C(2,-1),那么第四個頂點D的坐標(biāo)是( )| A. | (3,1) | B. | (3,2) | C. | (3,3) | D. | (3,4) |
分析 過B作BE⊥x軸于E,過D作DM⊥x軸于M,過C作CF⊥BE于F,DM和CF交于N,求出△DCN≌△BAE,根據(jù)全等三角形的性質(zhì)得出BE=DN,AE=CN,根據(jù)A、B、C的作求出OM和DM即可.
解答 解:
過B作BE⊥x軸于E,過D作DM⊥x軸于M,過C作CF⊥BE于F,DM和CF交于N,
則四邊形EFNM是矩形,
所以EF=MN,EM=FN,F(xiàn)N∥EM,
∴∠EAB=∠AQC,
∵四邊形ABCD是平行四邊形,
∴AB=DC,AB∥DC,
∴∠AQC=∠DCN,
∴∠DCN=∠EAB,
在△DCN和△BAE中
$\left\{\begin{array}{l}{∠N=∠BEA=90°}\\{∠DCN=∠EAB}\\{CD=AB}\end{array}\right.$
∴△DCN≌△BAE,
∴BE=DN,AE=CN,
∵A(-1,0)、B(-2,-3)、C(2,-1),
∴CN=AE=2-1=1,DN=BE=3,
∴DM=3-1=2,OM=2+1=3,
∴D的坐標(biāo)為(3,2),
故選B.
點評 本題考查了全等三角形的性質(zhì)和判定,平行四邊形的性質(zhì),點的坐標(biāo)與圖形性質(zhì)等知識點,能正確作出輔助線是解此題的關(guān)鍵.


 暑假作業(yè)海燕出版社系列答案
暑假作業(yè)海燕出版社系列答案 本土教輔贏在暑假高效假期總復(fù)習(xí)云南科技出版社系列答案
本土教輔贏在暑假高效假期總復(fù)習(xí)云南科技出版社系列答案 暑假作業(yè)北京藝術(shù)與科學(xué)電子出版社系列答案
暑假作業(yè)北京藝術(shù)與科學(xué)電子出版社系列答案科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,正方形ABCD中,BP=PQ=QC,AQ與DP交于R,若正方形ABCD的面積為100cm2,則△PQR的面積為 ( )cm2.
如圖,正方形ABCD中,BP=PQ=QC,AQ與DP交于R,若正方形ABCD的面積為100cm2,則△PQR的面積為 ( )cm2.| A. | 25 | B. | $\frac{50}{3}$ | C. | $\frac{25}{12}$ | D. | $\frac{25}{6}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 4或-4 | B. | 4 | C. | -4 | D. | 以上都不對 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,在 Rt△ABC中,∠ACB=90°,AC=BC=6 cm,點P從點A出發(fā),沿AB方向以每秒$\sqrt{2}$cm的速度向終點B運動;同時,動點Q從點B出發(fā)沿BC方向以每秒1 cm的速度向終點C運動.當(dāng)△PQC為等腰三角形時,則t的值為2.
如圖,在 Rt△ABC中,∠ACB=90°,AC=BC=6 cm,點P從點A出發(fā),沿AB方向以每秒$\sqrt{2}$cm的速度向終點B運動;同時,動點Q從點B出發(fā)沿BC方向以每秒1 cm的速度向終點C運動.當(dāng)△PQC為等腰三角形時,則t的值為2.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | m2-n2=(m-n)2 | B. | 3m2-6m-9=3(m-3)(m+1) | ||
| C. | x4-2x2y2+y4=(x2-y2)2 | D. | x2-3x-4=(x+4)(x-1) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 兩直線平行,同位角相等 | B. | 直線AB和直線CD不一定垂直 | ||
| C. | 若|a|=|b|,則a2=b2 | D. | 同角的補(bǔ)角相等 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 5,13,12 | B. | 2,3,$\sqrt{5}$ | C. | 4,7,5 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com