
分析 先對所求式子化簡,然后選取合適的x的值代入即可解答本題,注意x不能取-1,-2.
解答 解:(x-1-$\frac{3}{x+1}$)÷$\frac{{x}^{2}+4x+4}{x+1}$
=$(\frac{{{x^2}-1}}{x+1}-\frac{3}{x+1})×\frac{x+1}{{{{(x+2)}^2}}}$
=$\frac{(x+2)(x-2)}{x+1}×\frac{x+1}{{{{(x+2)}^2}}}$
=$\frac{x-2}{x+2}$
當x=0時,
原式=$\frac{0-2}{0+2}=-1$.
點評 本題考查分式的化簡求值,解題的關鍵是明確分式化簡求值的方法.


科目:初中數學 來源: 題型:填空題
 二次函數y=ax2+bx+c(a≠0)的部分圖象如圖所示,對稱軸為直線x=-1,與x軸的一個交點為(1,0),與y軸的交點為(0,3),則方程ax2+bx+c=0(a≠0)的解為x1=1,x2=-3.
二次函數y=ax2+bx+c(a≠0)的部分圖象如圖所示,對稱軸為直線x=-1,與x軸的一個交點為(1,0),與y軸的交點為(0,3),則方程ax2+bx+c=0(a≠0)的解為x1=1,x2=-3.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖a和b是相交于點O的兩條公路,A,B是兩個加油站,現準備在∠AOB的內部建一個油庫,要求油庫的位置點P既到A,B兩個加油站的距離相等,又到兩條公路a,b的距離相等,試用尺規作圖作出點P.
如圖a和b是相交于點O的兩條公路,A,B是兩個加油站,現準備在∠AOB的內部建一個油庫,要求油庫的位置點P既到A,B兩個加油站的距離相等,又到兩條公路a,b的距離相等,試用尺規作圖作出點P.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,以點O為圓心的兩個同心圓中,大圓的弦AB是小圓的切線,點P是切點,AB=12$\sqrt{3}$,OP=6,則大圓的半徑長為( )
如圖,以點O為圓心的兩個同心圓中,大圓的弦AB是小圓的切線,點P是切點,AB=12$\sqrt{3}$,OP=6,則大圓的半徑長為( )| A. | 6 | B. | 6$\sqrt{3}$ | C. | 6$\sqrt{2}$ | D. | 12 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
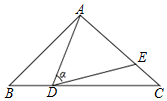 如圖,在△ABC中,AB=AC=10,BC=16,點D是邊BC上一動點(不與B,C重合),∠ADE=∠B=α,DE交AC于點E,下列結論:
如圖,在△ABC中,AB=AC=10,BC=16,點D是邊BC上一動點(不與B,C重合),∠ADE=∠B=α,DE交AC于點E,下列結論:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖所示,在△ABC中,已知點D,E,F分別是BC,AD,CE的中點,S△ABC=4平方厘米,則S△BEF的值為( )
如圖所示,在△ABC中,已知點D,E,F分別是BC,AD,CE的中點,S△ABC=4平方厘米,則S△BEF的值為( )| A. | 2平方厘米 | B. | 1平方厘米 | C. | $\frac{1}{2}$平方厘米 | D. | $\frac{1}{4}$平方厘米 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com