
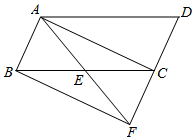
 如圖,已知E是平行四邊形ABCD中BC邊的中點,連接AE并延長AE交DC的延長線于點F.
如圖,已知E是平行四邊形ABCD中BC邊的中點,連接AE并延長AE交DC的延長線于點F.分析 (1)根據平行線的性質,可以利用AAS或ASA判斷.
(2)根據對角線相等的平行四邊形是矩形證明即可.
(3)結論:當△ABC為等腰三角形時,即AB=AC時,四邊形ABFC為正方形;根據鄰邊相等的矩形是正方形即可證明.
解答 證明:(1)∵四邊形ABCD為平行四邊形,
∴AB∥DC,
∴∠ABE=∠ECF,
∵E為BC的中點,
∴BE=CE,
在△ABE和△FCE中,
$\left\{\begin{array}{l}{∠ABE=∠ECF}\\{BE=CE}\\{∠AEB=∠FEC}\end{array}\right.$,
∴△ABE≌△FCE(ASA);
(2)∵△ABE≌△FCE,
∴BE=EC,AE=EF,
∴四邊形ABFC為平行四邊形,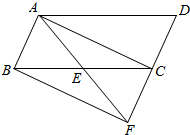
∵AE=$\frac{1}{2}$BC,
∴AF=BC,
∴四邊形ABFC為矩形(對角線相等的平行四邊形是矩形);
(3)當△ABC為等腰三角形時,即AB=AC時,四邊形ABFC為正方形;
理由如下:
由(2)可知四邊形ABFC是矩形,
∵AB=AC,
∴四邊形ABFC為正方形(鄰邊相等的矩形是正方形).
故答案為:AB=AC.
點評 本題考查了平行四邊形的判定與性質、矩形的判定、正方形的判定,全等三角形的性質和判定等知識,解題的關鍵是熟練掌握特殊四邊形的判定和性質,屬于中考常考題型.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:填空題
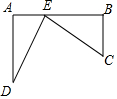 如圖,鐵路上A,B兩站(視為線上兩點)相距25千米,C,D為鐵路同旁兩個村莊(視為兩點),DA⊥AB于A點,CB⊥AB于B點,DA=15千米,CB=10千米,現在要在鐵路AB上修一個土特品回購站E,使C,D兩村莊到E站的距離相等,則E站應建在距A站10千米處.
如圖,鐵路上A,B兩站(視為線上兩點)相距25千米,C,D為鐵路同旁兩個村莊(視為兩點),DA⊥AB于A點,CB⊥AB于B點,DA=15千米,CB=10千米,現在要在鐵路AB上修一個土特品回購站E,使C,D兩村莊到E站的距離相等,則E站應建在距A站10千米處.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com