
 我市某工藝廠設計了一款成本為10元/件的工藝品投放市場進行試銷,經過市場調查,得到如下數據:
我市某工藝廠設計了一款成本為10元/件的工藝品投放市場進行試銷,經過市場調查,得到如下數據:| 銷售單價x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天銷售量y(件) | … | 500 | 400 | 300 | 200 | 100 | … |
分析 (1)利用描點法得出各點位置,進而利用待定系數法求一次函數解析式即可;
(2)利用銷量×單件利潤=總利潤,則W=(x-10)(-10x+700),因為x≤35,利用二次函數的增減性,結合對稱軸即可得出答案
解答 解:(1)畫圖如下: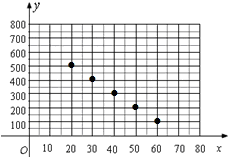
由圖可猜想y與x是一次函數關系,設這個一次函數為y=kx+b(k≠0),
∵這個一次函數的圖象經過(20,500)、(30,400)兩點,
∴$\left\{\begin{array}{l}{20k+b=500}\\{30k+b=400}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-10}\\{b=700}\end{array}\right.$.
∴函數關系式是y=-10x+700(10≤x≤70);
(2)由題意得:函數W=(x-10)(700-10x)
=-10(x-40)2+9000,
∵x≤35,
∴當x≤35時,W最大=8750,
∴銷售單價定為35元/件時,工藝廠試銷該工藝品每天獲得的利潤最大,最大利潤為8750元.
點評 此題主要考查了二次函數的應用以及一元二次方程的應用等知識,利用銷量×單件利潤=總利潤得出函數解析式是解題關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
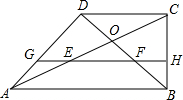 在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,對角線AC與BD相交于點O,線段OA,OB的中點分別為E,F.
在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,對角線AC與BD相交于點O,線段OA,OB的中點分別為E,F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
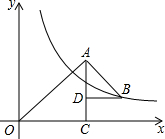 如圖,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函數y=$\frac{6}{x}$在第一象限的圖象經過點B,則△OAC與△BAD的面積之差S△OAC-S△BAD為( )
如圖,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函數y=$\frac{6}{x}$在第一象限的圖象經過點B,則△OAC與△BAD的面積之差S△OAC-S△BAD為( )| A. | 3 | B. | 6 | C. | 12 | D. | 36 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在△ABC中,點A1、A2是AB的三等分點,點B1、B2是BC的三等分點,點C1、C2、C3、C4是AC的五等分點,記四邊形A1A2C3C4、B1B2C1C2的面積分別為S1、S2,若S1+S2=12,則五邊形A2BB1C2C3的面積為14.
如圖,在△ABC中,點A1、A2是AB的三等分點,點B1、B2是BC的三等分點,點C1、C2、C3、C4是AC的五等分點,記四邊形A1A2C3C4、B1B2C1C2的面積分別為S1、S2,若S1+S2=12,則五邊形A2BB1C2C3的面積為14.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com