
分析 (1)通過理解題意可知本題的等量關系,即甲單獨修完這些桌凳的天數=乙單獨修完的天數+20天,列方程求解即可;
(2)分別求出三種方案的總費用,比較后即可得.
解答 解:(1)設該中學庫存x套桌椅,
則甲需要$\frac{x}{16}$天,乙需要$\frac{x}{16+8}$天,
根據題意得:$\frac{x}{16}$-$\frac{x}{16+8}$=20,
解得:x=960,
答:該中學庫存960套桌椅;
(2)方案a的費用為(80+10)×$\frac{960}{16}$=5400(元),
方案b的費用為(120+10)×$\frac{960}{16+8}$=5200(元),
方案c的費用為(80+120+10)×$\frac{960}{16+16+8}$=5040(元),
綜上,方案c的費用省時又省力.
點評 本題考查了一元一次方程的應用,解題的關鍵是找到等量關系:甲單獨修完這些桌凳的天數=乙單獨修完的天數+20天.


 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
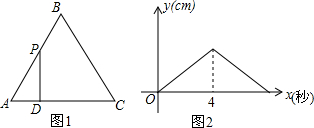
| A. | $\frac{5\sqrt{3}}{4}$cm | B. | $\frac{5\sqrt{3}}{2}$cm | C. | 2$\sqrt{3}$cm | D. | 3$\sqrt{3}$cm |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
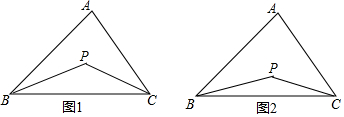 【提出問題】已知如圖1,P是∠ABC、∠ACB的角平分線的交點,你能找到∠P、∠A的關系嗎?
【提出問題】已知如圖1,P是∠ABC、∠ACB的角平分線的交點,你能找到∠P、∠A的關系嗎?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
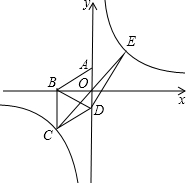 如圖,在平面直角坐標系中四邊形ABCD為菱形,邊AD在y軸上.其中A(0,1),B(-$\sqrt{3}$,0),雙曲線y=$\frac{m}{x}$經過點C.
如圖,在平面直角坐標系中四邊形ABCD為菱形,邊AD在y軸上.其中A(0,1),B(-$\sqrt{3}$,0),雙曲線y=$\frac{m}{x}$經過點C.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com