Question

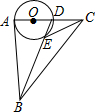
4．如圖，△ABC中，∠BAC=90°，AB=AC=2，D為AC上一動點，以AD為直徑的⊙O交BD于E，則線段CE的最小值為（　　）

• A． $\sqrt{5}$
• B． $\sqrt{5}$+1
• C． 2$\sqrt{5}$
• D． $\sqrt{5}$-1

Answer 1

分析 連接AE，可得∠AED=∠BEA=90°，從而知點E在以AB為直徑的⊙Q上，繼而知點Q、E、C三點共線時CE最小，根據(jù)勾股定理求得QC的長，即可得線段CE的最小值．

解答 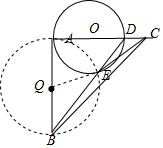解：如圖，連接AE，則∠AED=∠BEA=90°，
∴點E在以AB為直徑的⊙Q上，
∵AB=2，
∴QA=QB=1，
當點Q、E、C三點共線時，CE最小，
∵AC=2，
∴QC=$\sqrt{5}$，
∴CE=QC-QE=$\sqrt{5}$-1，
故選：D．

點評 本題考查了圓周角定理和勾股定理的綜合應用，解決本題的關(guān)鍵是確定E點運動的軌跡，從而把問題轉(zhuǎn)化為圓外一點到圓上一點的最短距離問題．