
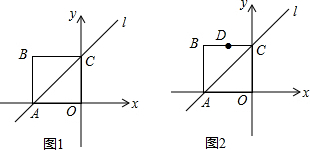
���� ��1����D1�У����ֱ��l�Ľ���ʽ��y=x+2���O(sh��)�c(di��n)P������(bi��o)�飨m��m+2�������}���$\frac{1}{2}$��2��|m+2|=3���ⷽ�̼��ɣ�
��2����D2�У��B��OD��ֱ��l���c(di��n)E���t�c(di��n)E�����˕r(sh��)|BE+DE|=|OE+DE|=OD��OD�������ֵ�����ֱ��OD�Ľ���ʽ�����÷��̽M�����E����(bi��o)���ɣ�
��3����D3�У�O�cB�P(gu��n)��ֱ��l��(du��)�Q������BE=OE��|BE-DE|=|OE-DE|���Ƀ�߅֮��С�ڵ���߅֪����(d��ng)�c(di��n)O��D��E���c(di��n)�����r(sh��)��|OE-DE|��ֵ������ֵ��OD�����ֱ��OD�Ľ���ʽ�����÷��̽M������c(di��n)E����(bi��o)���ɣ�
��� �⣺��1����D1�У�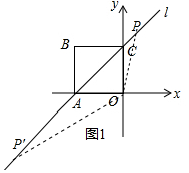
���}��֪�c(di��n)A���c(di��n)C������(bi��o)�քe�飨-2��0���ͣ�0��2��
�O(sh��)ֱ��l�ĺ���(sh��)���_(d��)ʽy(t��ng)=kx+b��k��0������(j��ng)�^(gu��)�c(di��n)A��-2��0�����c(di��n)C��0��2����
��$\left\{\begin{array}{l}{-2k+b=0}\\{b=2}\end{array}\right.$���$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$��
��ֱ��l�Ľ���ʽ��y=x+2��
�O(sh��)�c(di��n)P������(bi��o)�飨m��m+2����
���}���$\frac{1}{2}$��2��|m+2|=3����m=1��m=-5��
��P��1��3����P�䣨-5��-3����
��2����D2�У��B��OD��ֱ��l���c(di��n)E���t�c(di��n)E�����˕r(sh��)|BE+DE|=|OE+DE|=OD��OD�������ֵ��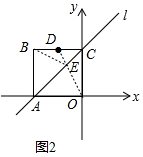
�O(sh��)OD����ֱ����y=k1x��k1��0������(j��ng)�^(gu��)�c(di��n)D��-1��2����
��2=-k1��
��k1=-2��
��ֱ��OD��y=-2x��
��$\left\{\begin{array}{l}{y=x+2}\\{y=-2x}\end{array}\right.$ ���$\left\{\begin{array}{l}{x=-\frac{2}{3}}\\{y=\frac{4}{3}}\end{array}\right.$��
���c(di��n)E������(bi��o)�飨-$\frac{2}{3}$��$\frac{4}{3}$����
�֡��c(di��n)D������(bi��o)�飨-1��2����
���ɹ��ɶ����ɵ�OD=$\sqrt{5}$��
��|BE+DE|����Сֵ��$\sqrt{5}$��
��3����D3��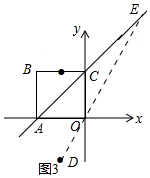
��O�cB�P(gu��n)��ֱ��l��(du��)�Q��
��BE=OE����|BE-DE|=|OE-DE|��
�Ƀ�߅֮��С�ڵ���߅֪����(d��ng)�c(di��n)O��D��E���c(di��n)�����r(sh��)��|OE-DE|��ֵ������ֵ��OD��
��D��-1��-2����
��ֱ��OD�Ľ���ʽ��y=2x��OD=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$��
��$\left\{\begin{array}{l}{y=2x}\\{y=x+2}\end{array}\right.$�����$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$��
���c(di��n)E��2��4����
��|BE-D��E|�����ֵ��$\sqrt{5}$�˕r(sh��)�c(di��n)E������(bi��o)�飨2��4����
�c(di��n)�u(p��ng) ���}������߅�ξC���}��һ�κ���(sh��)�đ�(y��ng)�á������ε����|(zh��)�������ε���e�����ɶ�����֪�R(sh��)�����}���P(gu��n)�I�njW(xu��)��(hu��)���Ì�(du��)�Q������(j��)���c(di��n)֮�g������̣���Q��Сֵ��(w��n)�}������(j��)�����εă�߅֮��С�ڵ���߅���_�����ֵ��(w��n)�}�������п������}�ͣ�



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
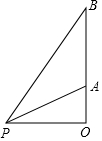 ��D��һö����ĵ���O̎�l(f��)�䣬�ھ��x�l(f��)���c(di��n)9km̎�ĵ����^�y(c��)վP�c(di��n)�y(c��)�û���ײ����_(d��)A�c(di��n)�r(sh��)����ײ������Ǟ�30�㣻20s�����ײ����_(d��)B�c(di��n)���y(c��)����ײ������Ǟ�60�㣮���@ö�����A�c(di��n)��B�c(di��n)��ƽ���ٶȣ����_�� 0.1km/s����������(sh��)��(j��)��$\sqrt{2}$��1.41��$\sqrt{3}$��1.73��$\sqrt{5}$��2.24��
��D��һö����ĵ���O̎�l(f��)�䣬�ھ��x�l(f��)���c(di��n)9km̎�ĵ����^�y(c��)վP�c(di��n)�y(c��)�û���ײ����_(d��)A�c(di��n)�r(sh��)����ײ������Ǟ�30�㣻20s�����ײ����_(d��)B�c(di��n)���y(c��)����ײ������Ǟ�60�㣮���@ö�����A�c(di��n)��B�c(di��n)��ƽ���ٶȣ����_�� 0.1km/s����������(sh��)��(j��)��$\sqrt{2}$��1.41��$\sqrt{3}$��1.73��$\sqrt{5}$��2.24���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
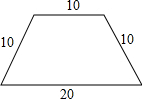 ��һ���������εĻh�ʣ����ĸ�߅�L(zh��ng)��D��ʾ������������̎�������ć���һ��(g��)�L(zh��ng)���λh�ʣ�ʹ�Ç��ɵ��L(zh��ng)���ε�һ߅�L(zh��ng)��10���t�˕r(sh��)�h�ʇ��ɵ��L(zh��ng)���ε���һ߅�L(zh��ng)����٣����ć���һ��(g��)�����εĻh�ʣ������ε�߅�L(zh��ng)����٣������^�������L(zh��ng)���κ��������Ă�(g��)��e����
��һ���������εĻh�ʣ����ĸ�߅�L(zh��ng)��D��ʾ������������̎�������ć���һ��(g��)�L(zh��ng)���λh�ʣ�ʹ�Ç��ɵ��L(zh��ng)���ε�һ߅�L(zh��ng)��10���t�˕r(sh��)�h�ʇ��ɵ��L(zh��ng)���ε���һ߅�L(zh��ng)����٣����ć���һ��(g��)�����εĻh�ʣ������ε�߅�L(zh��ng)����٣������^�������L(zh��ng)���κ��������Ă�(g��)��e�����鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com