
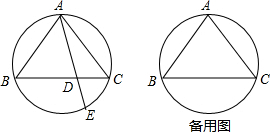
分析 (1)連接BE,由等腰三角形的性質(zhì)和圓周角定理證出∠ABC=∠E,證明△ABD∽△AEB,得出對(duì)應(yīng)邊成比例即可;
(2)由圓內(nèi)接四邊形的性質(zhì)和鄰補(bǔ)角證出∠AEC=∠ACD,證明△ACE∽△ADC,得出對(duì)應(yīng)邊成比例證出AC2=AD•AE,即可得出結(jié)論.
解答 (1)證明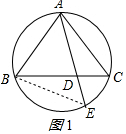 :連接BE,如圖1所示:
:連接BE,如圖1所示:
∵AB=AC,
∴∠ABC=∠C,
∵∠E=∠C,
∴∠ABC=∠E,
又∵∠BAD=∠EAB,
∴△ABD∽△AEB,
∴AB:AE=AD:AB,
∴AB2=AD•AE;
(2)解:(1)中的結(jié)論還成立;理由如下: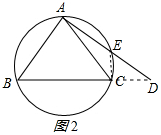
如圖2所示:連接CE,
∵∠ABC+∠AEC=180°,∠ACD+∠ACB=180°,∠ABC=∠ACB,
∴∠AEC=∠ACD,
又∵∠CAE=∠DAC,
∴△ACE∽△ADC,
∴AC:AD=AE:AC,
∴AC2=AD•AE,
∵AB=AC,
∴AB2=AD•AE.
點(diǎn)評(píng) 本題考查了相似三角形的判定與性質(zhì)、等腰三角形的性質(zhì)、圓周角定理、圓內(nèi)接四邊形的性質(zhì)等知識(shí);證明三角形相似是解決問題的關(guān)鍵.


 能考試期末沖刺卷系列答案
能考試期末沖刺卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1個(gè) | B. | 2個(gè) | C. | 3個(gè) | D. | 4個(gè) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
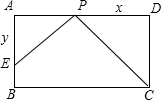 已知矩形ABCD中,CD=2,AD=3,點(diǎn)P是AD上的一個(gè)動(dòng)點(diǎn),且和點(diǎn)A,D不重合,過點(diǎn)P作PE⊥CP,交邊AB于點(diǎn)E,設(shè)PD=x,AE=y,求y關(guān)于x的函數(shù)關(guān)系式,并寫出x的取值范圍.
已知矩形ABCD中,CD=2,AD=3,點(diǎn)P是AD上的一個(gè)動(dòng)點(diǎn),且和點(diǎn)A,D不重合,過點(diǎn)P作PE⊥CP,交邊AB于點(diǎn)E,設(shè)PD=x,AE=y,求y關(guān)于x的函數(shù)關(guān)系式,并寫出x的取值范圍.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
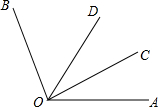 如圖,∠AOC=30°35′25″,∠BOC=80°15′28″,OC平分∠AOD,那么∠BOD等于49°40′3″.
如圖,∠AOC=30°35′25″,∠BOC=80°15′28″,OC平分∠AOD,那么∠BOD等于49°40′3″.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com