
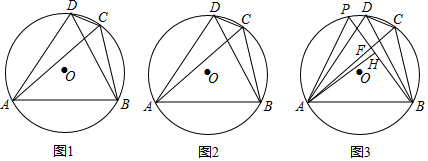
分析 (1)欲證明AD=BD,只要證明∠DAB=∠DBA即可.
(2)如圖2中,延長DC到G,使得CG=CB,連接BG.首先證明△ABD,△CBG是等邊三角形,再證明△DBG≌△ACB即可.
(3)如圖3中,作連接CE,連接AE、BE.首先證明△BEC是等腰直角三角形,由∠PAH=30°,推出PA=2PH,AH=$\sqrt{3}$PH,設PF=a,FH=4x,則BH=21x,FB=25x,推出PA=2(a+4x),AH=$\sqrt{3}$(a+4x),在Rt△AHF中,由AF2=FH2+AH2,推出AF=$\sqrt{(4x)^{2}+[\sqrt{3}(a+4x)]^{2}}$,由△PAF∽△CBF,得$\frac{PA}{CB}$=$\frac{FA}{FB}$,$\frac{2(a+4x)}{5\sqrt{2}}$=$\frac{\sqrt{(4x)^{2}+[\sqrt{3}(a+4x)]^{2}}}{25x}$,即50x2(a+4x)2=16x2+3(a+4x)2 ①,在Rt△ABH中,AH2+BH2=AB2,推出[$\sqrt{3}$(a+4x)]2+(21x)2=(5$\sqrt{3}$)2,即(a+4x)2=25-147x2 ②,解方程組即可解決問題.
解答 (1)證明:如圖1中,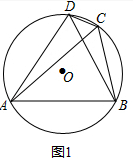
∵∠DCA+∠DCB=180°,又∵∠DCB+∠DAB=180°,
∴∠DCA=∠DAB,
∵∠DCA=∠ABD,
∴∠DAB=∠ABD,
∴DA=BD.
(2)證明:如圖2中,延長DC到G,使得CG=CB,連接BG.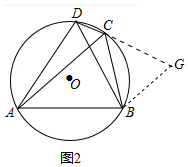
∵∠BCA=60°,
∴∠ADB=∠ACB=60°,∵DA=DB,
∴△ADB是等邊三角形,
∴∠DAB=60°,∠DCB=180°-∠DAB=120°,
∴∠BCG=60°,∵CG=CB,
∴△BCG是等邊三角形,
∴∠G=∠ACB=60°,∠CAB=∠BDG,
在△DBG和△ACB中,
$\left\{\begin{array}{l}{∠G=∠ACB}\\{∠BDG=∠BAC}\\{AB=BD}\end{array}\right.$,
∵△DBG≌△ACB(ASA),
∴DG=AC,
∴AC=DC+CG=DC+BC.
(3)解:如圖3中,作連接CE,連接AE、BE.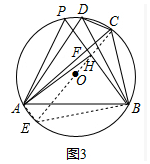
∵△ADB是等邊三角形,⊙O半徑為5,
∴AB=AD=BD=5$\sqrt{3}$,
∵∠CAE=90°,
∴CE是直徑,
∴∠EBC=90°,
∵CD=AE,
∴$\widehat{CD}$=$\widehat{AE}$,
∵$\widehat{DCB}$=$\widehat{AEB}$,
∴$\widehat{BC}$=$\widehat{EB}$,
∴BC=BE,
∵CE=10,
∴EB=BC=5$\sqrt{2}$,
∵∠P=∠ADB=∠ACB=60°,AH⊥PB,
∴∠PAH=30°,
∴PA=2PH,AH=$\sqrt{3}$PH,設PF=a,FH=4x,則BH=21x,FB=25x,
∴PA=2(a+4x),AH=$\sqrt{3}$(a+4x),
在Rt△AHF中,∵AF2=FH2+AH2,
∴AF=$\sqrt{(4x)^{2}+[\sqrt{3}(a+4x)]^{2}}$,
∵∠P=∠ACB=60°,∠PAF=∠CBF,
∴△PAF∽△CBF,
∴$\frac{PA}{CB}$=$\frac{FA}{FB}$,
∴$\frac{2(a+4x)}{5\sqrt{2}}$=$\frac{\sqrt{(4x)^{2}+[\sqrt{3}(a+4x)]^{2}}}{25x}$,
即50x2(a+4x)2=16x2+3(a+4x)2 ①
在Rt△ABH中,AH2+BH2=AB2,
∴[$\sqrt{3}$(a+4x)]2+(21x)2=(5$\sqrt{3}$)2,
即(a+4x)2=25-147x2 ②
把②代入①得50x2(25-147x2)=16x2+75-212x2,
整理得294x4-67x2+3=0,
∴(49x2-3)(6x2-1)=0,
∴x2=$\frac{3}{49}$或(x2=$\frac{1}{6}$不合題意舍棄),
把x2=$\frac{3}{49}$代入②得,(a+4x)2=25-9=16,
∴a+4x=4,
∴2(a+4x)=8.
∴AP=8.
點評 本題考查圓綜合題、等腰三角形的判定和性質、等邊三角形的判定和性質、全等三角形的判定和性質、相似三角形的判定和性質等知識,解題的關鍵是學會添加常用輔助線,構造全等三角形,學會利用參數,構建方程,利用方程組解決問題,屬于中考壓軸題.


科目:初中數學 來源: 題型:填空題
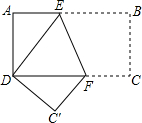 在長方形紙片ABCD中,AD=6cm,AB=8cm,按如圖方式折疊,使點B與點D重合,折痕為EF,則EF的長為$\frac{15}{2}$.
在長方形紙片ABCD中,AD=6cm,AB=8cm,按如圖方式折疊,使點B與點D重合,折痕為EF,則EF的長為$\frac{15}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在平面直角坐標系中,?ABOC如圖放置,點C的坐標是(-1,0),點A在y軸的正半軸上,將此平行四邊形繞點O順時針旋轉90°,得?A′B′OC′,拋物線y=ax2+bx+4過點C、A、A′,點M是此拋物線的一動點,設點M的橫坐標為m.
在平面直角坐標系中,?ABOC如圖放置,點C的坐標是(-1,0),點A在y軸的正半軸上,將此平行四邊形繞點O順時針旋轉90°,得?A′B′OC′,拋物線y=ax2+bx+4過點C、A、A′,點M是此拋物線的一動點,設點M的橫坐標為m.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
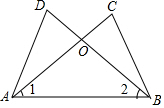 如圖,AC、BD相交于點O,∠1=∠2,若用“SAS”說明△ACB≌△BDA,則還需要加上條件( )
如圖,AC、BD相交于點O,∠1=∠2,若用“SAS”說明△ACB≌△BDA,則還需要加上條件( )| A. | AD=BC | B. | BD=AC | C. | ∠D=∠C | D. | OA=AB |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
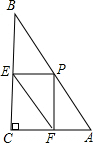 如圖,直角三角形ABC中,AC=1,BC=2,P為斜邊AB上一動點.PE⊥BC,PF⊥CA,則線段EF長的最小值為$\frac{2}{5}\sqrt{5}$.
如圖,直角三角形ABC中,AC=1,BC=2,P為斜邊AB上一動點.PE⊥BC,PF⊥CA,則線段EF長的最小值為$\frac{2}{5}\sqrt{5}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com